Talk about where oil prices are headed is cheap, so at least we have plenty of that. But how
seriously does the market take the various possibilities that are being bandied about by the
pundits?
No matter what you think is about to happen to oil prices, there’s somebody out there who
agrees with you.
John
Murphy sees a 70-80% chance oil will go to $70 a barrel
(hat tip: Land of Black
Gold).
That’s much too tame a forecast for Matthew
Simmons, who thinks oil could be at $100 within six months. On the other hand, Stephen Ayer at
Disinterested Party wants to put his money on $40 a barrel. And Tim Worstall
declares flatly that the oil market is in a bubble.
I earlier talked
about how you could use an oil futures contract to get rich if you think you have a good
idea where oil prices are headed, and here I’d like to describe a different way to make money if
you think there’s some chance that a particular one of these pundits has it right. You can
purchase a contract on the New York
Mercantile Exchange which
gives you the right to buy a futures contract for 1,000 barrels of oil, for delivery in June
2006, at a price of $80 a barrel. Such a contract is known as an $80 call option. Unlike a
regular futures contract, in which you have to buy the oil for $80, with the call option, you
only have to buy the oil if you decide later that you really want to. Today’s closing price for
buying this $80 June 2006 call option was $2.41 a barrel. If oil doesn’t go above $80 within
the next 12 months, and you don’t try to sell the option to somebody else in the mean time, the
option to buy oil for $80 next year will turn out to be worthless, and you’ve just thrown away
$2,410. But if Matthew Simmons is right and oil goes to $100 a barrel, by buying oil next June
for $80 (as you’ve entitled yourself through the option) and selling it for $100 (where Simmons
says it will be), you’ve made $17,590 profit on your initial investment of $2,410.
If there’s better than a 14% chance that Simmons is right, on average you’ll come out ahead
making this kind of deal (0.14 x $17,590 = $2,463 > $2,410). On the other hand, the person on
the other end of the deal, who sold you the option, probably thinks the chance is well under
14%.
This is a rather simplistic way of thinking about the probabilities, because oil might not
get all the way to $100, but still could make it up to $90, in which case you’d still make
plenty of profit if you had purchased that option. For this reason, you might well want to buy
that $80 June 2006 option even if you thought there was much less than a 14% chance of oil going
over $100. To do the calculation correctly, you’d need to spell out a complete probability
distribution, and see how you’d fare with the option for each possible outcome. One common
model that many traders use is to suppose that the change in the natural logarithm of oil prices
over any length of time t is normally distributed with mean m times t and variance s2
times t. If for simplicity you also figured that you wouldn’t plan on exercising the option
until a year from now, then a formula developed by Fischer Black and Myron Scholes can be used
to calculate just how much you should be willing to pay for the option. A convenient program to
do those calculations can be run on-line. You
input the current price of the June 2006 futures contract
($62.04 a barrel on today’s close), the interest rate for the calculation, and the standard
deviation s that characterizes how you view the probability distribution, and it will calculate
for you how much it would make sense for someone with your beliefs to pay for that $80 call
option; (it turns out that from the Black-Scholes calculations, it’s only the standard deviation
s, not the mean m, that determines the value of the option). Alternatively, you can figure
out, given that somebody’s willing to sell you the option for $2.41, what value of s is being
assumed by the person offering to sell you the option at the price of $2.41. For the $80 June
2006 call option, the implied value for s is about 33%. This number is referred to as the
“implied volatility” of the option.
Or, if you’re thinking more along the lines of Stephen Ayer or Tim Worstall, you might be
interested in an option such as the $50 put. Here you’d pay somebody $2.39 per barrel today,
and they’re committed to buy oil from you at $50 a barrel next year, if you choose to hold them
to it. If Simmons is right, of course you’re not going to want to sell oil next year at
anything like $50, and that $2.39 you spent will have been wasted. But if Ayer or Worstall are
right, you’ll make a dandy profit. Again the value of s implied by the $2.39 valuation of that
$50 June 2006 put option turns out to be s = 33%. You’d come up with a pretty similar value for
s looking at most of the call or put options available for trade.
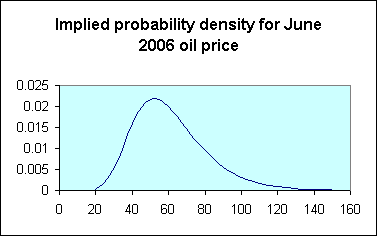
As you get into options that would only be exercised in a very dramatic turn in the market,
such as the $100 call or $30 put options, it turns out that the seller of that option would ask
for a price that is a little higher than would be expected for a distribution with standard
deviation of s = 0.33, and corresponds instead to a value of s more like 0.36. This is
something you very often find for these calculations, and is referred to as the “volatility
smile.” The volatility smile is used to describe the phenomenon that, as you look at options
whose strike price is farther and farther away from June 2006 futures price itself, the implied
volatility gets a little higher. This smile shape may reflect the fact that traders view oil
price changes as coming from a distribution with fatter tails than the lognormal distribution from
which the Black-Scholes formula is derived. I’ve used that s = 0.36 value along with the
futures price to set the mean m to illustrate this implied probability density for the June 2006
price of oil in the above figure, and tabulated the probability that this implies that the June
2006 oil price would be below any particular value P in the table below. The market is putting
something like a 7% chance that oil will go above Simmons’s $100, and a 15% chance it could go
below Ayer’s $40.
| Price (P) ($ per barrel) | Probability that price will be below P |
|---|---|
| 30 | 0.03 |
| 40 | 0.15 |
| 50 | 0.34 |
| 60 | 0.54 |
| 70 | 0.70 |
| 80 | 0.81 |
| 90 | 0.89 |
| 100 | 0.93 |
I should perhaps also relate these calculations to what some of you may have seen in a story
first run by Bloomberg, which has
been picked up by Green
Car Congress,
Peak
Oil Optimist and today by a large number of news services. The Bloomberg story might have
seemed to suggest that recent trading in these oil options signifies a widespread belief among
traders that oil prices are going to rise dramatically. The primary evidence that the Bloomberg
article pointed to was the volume, which measures the number of people who bought an $80
December 2005 option. But what the article leaves out is that this is in fact the same as the
number of people who sold this option, and those folks are betting oil prices
aren’t going up that far. What’s relevant is not the volume but rather the price of
the transactions, and the price to which buyers and sellers agreed implies that, more likely
than not, oil is not going to reach $80 any time soon.
Could Matt Simmons still turn out to be right? He sure could. And if you think there’s,
say, a 20% chance that he will be, you should get on the phone right away to go after one of
those call options. You’ll find a rich capitalist on the other end, who aspires to become an
even richer capitalist, who will be more than happy to take the other side of that bet.
Superb post. As a futures professional, wanted to note that your series of articles wrt oil and the trading thereof, have been good reads.
Query/request – an article about futures price distortion due to “always long” index funds.
I disagree with above. Boone Pickens makes a persuasive argument to the effect that world demand is increasing and (in the near term) there is little prospect that supply can keep up … AND … that prospects for “something negative” (crisis in Venezuala, Nigeria, pipeline/refinery damage, etc) are ever so much greater than for “something positive” (a new oll field being brought on line, etc).
Mr Pickens predicts $100/bbl price prior to end of 2006.
How do you get the other numbers for the online Black-Scholes calculator? This is fascinating, but I’m not an economist and want to play around with the calculator.
Thanks.
Even if you assume that Mr. Pickens is correct about the relative probability of positive and negative events influencing the price, that still does not necessarily say anything about what the market price will be at any particular point in time.
It’s often not hard to know which way the market is going _in the long run_…but you can still lose plenty of money assuming it’ll do something similar in the short run.
I’d rate the odds of it hitting $100 in the next year quite a bit higher than the odds of any kind of substantial fall…but not so high I’d be willing to bet on it being $100 on any particular day.
I am afraid you are confusing risk-neutral measure and physical measure. Probabilities implied by option prices are NOT the consensus probabilities of the market. This may sound a bit technical, but the difference is huge.
For example, consider a stock worth $100 now, and suppose everybody believes that in one year it can only go up $10 (with probability 70%) or down $10 (with probability 30%), and assume that the interest rate is 0. It is easy ot see that the $100 strike call is worth $5: if one buys this call and sells 1/2 share then one gets $5 in one year with no risk. On the other hand, expected payoff on this call is 70%*($110-$100) = $7. Option prices are driven by no-arbitrage conditions, not by expected payoffs.
Will oil prices top $100 a barrel?
Prior posts here and here have highlighted the work of University of California at San Diego profeesor James D. Hamilton, who is one of the country’s foremost experts on the economics of energy prices. In this recent post, Professor Hamilton…
I agree with mic in the previous comment. The option prices are set by market expectations about volatility and do not reflect the odds of any particular price level.
The market’s expectations of future prices are imbedded in the spot price of the asset and not in the options prices.
Catching my eye: morning A through Z
Here’s what’s caught my eye this morning: The big news this morning is, of course, what now appears to be a terrorist attack on London transport. Your best source for information is The Command Post. KipEsquire of A Stitch in…
I don’t think I’m confused about this, Mic, but I’m happy to use your comment as an opportunity to try to be a little more clear.
The Black-Scholes formula is derived from the no-arbitrage condition associated with a particular dynamic hedge, and Mic gives a very nice example of why option prices have to satisfy these kinds of conditions. By the nature of the particular dynamic hedge considered by Black-Scholes, all that the condition ends up allowing you to infer is the variance of the distribution. In Mic’s example, if instead the price could be up 20 or down 20, the option would be worth 10, not 5. So in Mic’s example, you could infer from the option price the spread of the distribution but not the particular probabilities. In my analysis, I was only using the option price to get the variance of the density that I plotted, and was coming up with the mean separately from the futures price itself. It is true that the assumptions you need to make in order to infer the variance from the option price are different from the assumptions you need to make in order to infer the mean from the futures price. To use Black-Scholes, you need to assume a lognormal diffusion, whereas to use the futures price, you need to assume risk neutrality. I was making both sets of assumptions and using both markets in order to make statements about the full probability distribution.
A particular person such as Simmons or Ayer or the intended reader of my post has an opinion about both the mean and the variance, so a particular person would have an opinion about whether buying or selling a particular option at a particular price might or might not be a good deal. Since those opinions were the focus of my post, that is how I chose to organize my presentation.
Here’s more on how to use that Black-Scholes calculator, Dan. For “current future price” you put in the price you’d have to pay right now for the underlying futures contract on which you’re looking at an option. In my first example, I was looking at an option on the June 2006 futures contract, and the closing price on Tuesday for the June 2006 futures contract was $62.04. For “option strike price” you put in the strike price of the option you’re considering, for example, input 80 for the $80 June 2006 call option. For “days to expiration” you enter the number of days between now and the date of expiration of the contract you’re looking at. For example, the June 2006 contract expires on May 22, 2006, which is 319 days from now. For “annual interest rate” you want the risk-free rate, which you’d get from a Treasury security at 3.5%. For “price volatility” you put in the value of s quoted in percent, for example, for s = 0.33, you’d enter 33. If you put in those values, you’ll get a price for the call option of $2.41, which is what that option in fact sold for on Tuesday’s close, confirming that the implied volatility on that option was 33%.
Is there any data on how well options predicted large swings in oil prices?
Coming at this with no experience whatsoever, I would think the long term strategy would be to plot a fairly gradual increase in price, and hedge that position. occasionally, you might be losing money, such as in the big swings, but that on average, swings are predicted more than they materialize, leading the institutional strategies towrds a conservative path that grants that they will lose in the rare big swing scenarios.
Coach, one thing you can do is compare the volatility that’s implied by the current option prices with what the volatility of crude oil price changes has been historically. If you look at the standard deviation of changes in the log of crude oil prices going back to 1974, you end up with a historical volatility of 29%, a bit below the 33-36% implied volatility as currently priced in the market. So, the market is a bit more concerned about the possibility of a big move up or down at the moment than you would have been if you drew a month at random over the last quarter century.
The discussion given is confusing, because it suggests that the derivation of the option-implied probabilities depends on the Black-Scholes model. In fact, one can obtain these probabilities directly from the option prices.
For example, suppose that we wish to find the option-implied probability that oil is over $70 in December. If we are long a $69 call, and short a $70 call, we get paid $1 if oil is over $70, and $0 if oil is under $69. (For clarity, let’s ignore the case where oil is between $69 and $70.) The (risk-neutral) price of this position in cents is the percentage chance that this position pays off, i.e. that oil is above $70 in December.
The price of this position, as of this writing, is $3.24-2.95, or 29 cents, which gives an option-implied probability of 29%. Note that this is very close to the 30% one gets from the table in the original post.
For further discussion of this point, and the point made by mic above, readers may consult, for example, “The Concepts and Practice of Mathematical Finance”, by Mark Joshi, Ch. 6, Sec. 3.
It’s worth noting that Joshi restates mic’s point in a number of ways. Perhaps the clearest is “we can regard [the option-implied probability] as the probability the market is choosing to price with.”
$75-$85 bbl. No higher.
Ever bet those football pools at work?
Amazing how accurate those point spreads are.
Not if but when on $80 oil
It would be a lot easier if the discussion on whether or not we will see $80 a barrrel oil this year, and $3.50 a gallon gas, depended only on the availability of the refined product. Unfortunately it does not
Let’s Talk About Credit and Oil!
From the PrudentBear, there is a discussion of the Global Credit Bubble. This bubble has been primarily a US/Asian phenomenom with huge money flows between the US and China/Japan. As I have posted about recently, China’s reserves are to top $900 Bil…