Recently I’ve heard a number of otherwise intelligent people assess an economic hypothesis based on the R2 of an estimated regression. I’d like to point out why that can often be very misleading.
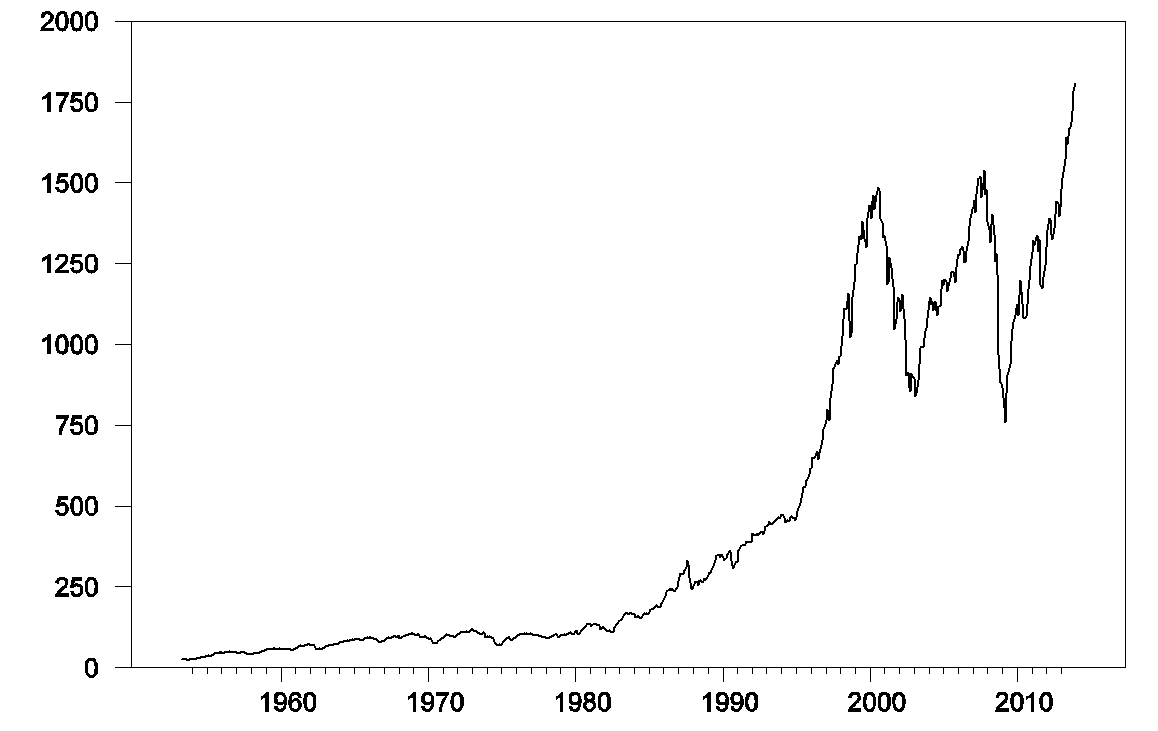 |
The above graph plots the S&P500 stock price index since 1953. Here’s what you’d find if you calculated a regression of this month’s stock price (pt) on last month’s stock price (pt-1). Standard errors of the regression coefficients are in parentheses.
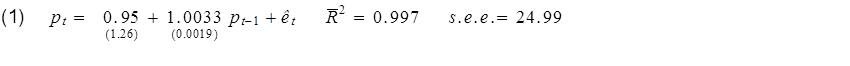
The adjusted R-squared for this relation is 0.997. One minus the R-squared is basically a summary of how large on average the squared residual of the regression is relative to the squared difference of the stock price from its historical mean. The latter is huge. For example, in December the S&P500 reached 1808, compared to its sample mean of 459. The square of that difference is (1808 – 459)2 = 182,000, which completely dwarfs the average squared regression residual (252 = 625). So if you’re a fan of getting a big R-squared, this regression is for you.
On the other hand, another way you could summarize the same relation is by using the change in the stock price (Δpt = pt – pt-1) as the left-hand variable in the regression:
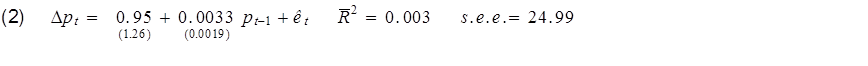
This is in fact the identical model of stock prices as the first regression. The standard errors of the regression coefficients are identical for the two regressions, and the standard error of the estimate (a measure of the standard deviation of the regression residual et) is identical for the two regressions because indeed the residuals are identical for every observation. Yet if we summarize the model using the second regression, the R-squared is now comparing those squared residuals not with squared deviations of pt from its sample mean, but instead with squared deviations of Δpt from its sample mean. The latter is much, much smaller, so the R-squared goes from almost one to almost zero.
Whatever you do, don’t say that the first model is good given its high R-squared and the second model is bad given its low R-squared, because equations (1) and (2) represent the identical model.
This is not simply a feature of the trend in stock prices over time. Here for example is a plot of the interest rate on 10-year Treasury bonds, whose values today are not that far from where they were in the 1950s:
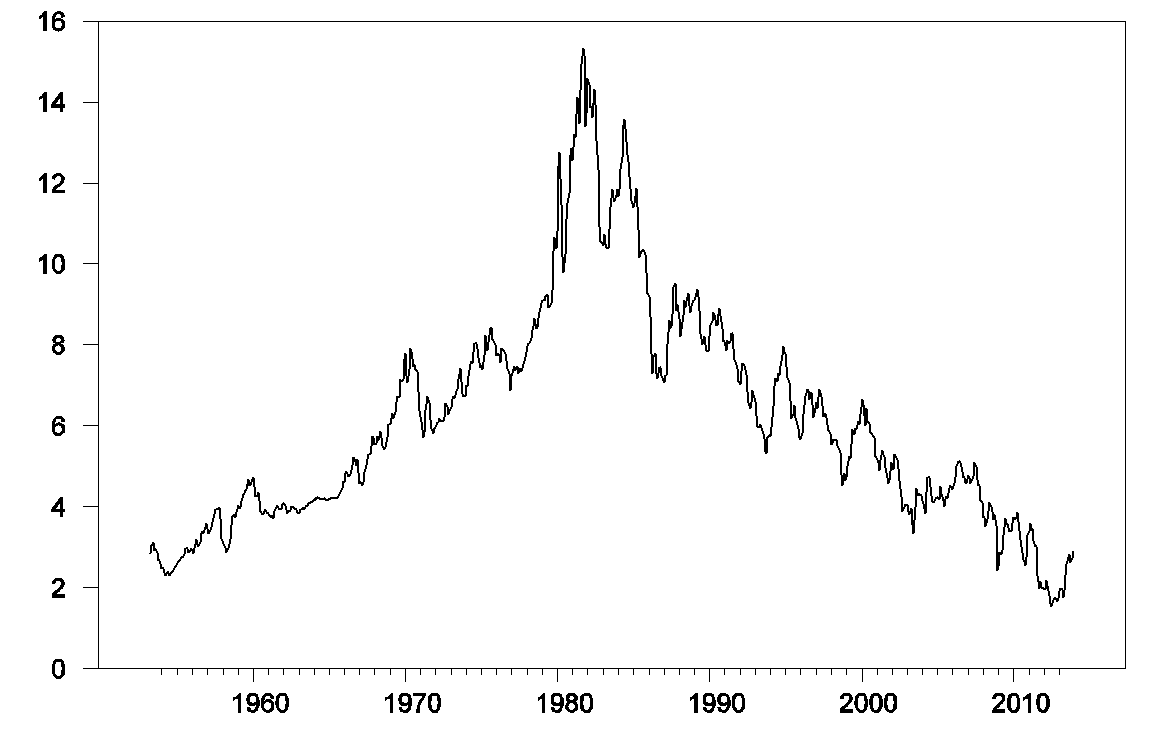 |
If you regress the interest rate on its values from the previous three months, you will get an R-squared of 0.992.
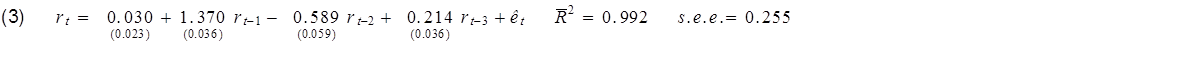
Or if you wanted to, you could describe exactly the same model by using the change in interest rates as the left-hand variable and report an R-squared of only 0.136:
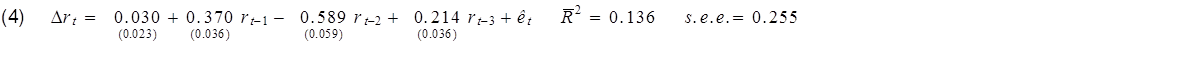
Note by the way that regression (2) above reproduces a common finding, which is, if you regress the change in stock prices on most variables you could have known at time t – 1, you usually get an R-squared near zero and coefficients that are statistically indistinguishable from zero. Is the failure to get a big R-squared when you do the regression that way evidence that economists don’t understand stock prices? Actually, there’s a well-known theory of stock prices that claims that an R-squared near zero is exactly what you should find. Specifically, the claim is that everything anybody could have known last month should already have been reflected in the value of pt -1. If you knew last month, when pt-1 was 1800, that this month it was headed to 1900, you should have bought last month. But if enough savvy investors tried to do that, their buy orders would have driven pt-1 up closer to 1900. The stock price should respond the instant somebody gets the news, not wait around a month before changing.
That’s not a bad empirical description of stock prices– nobody can really predict them. If you want a little fancier model, modern finance theory is characterized by the more general view that the product of today’s stock return with some other characteristics of today’s economy (referred to as the “pricing kernel”) should have been impossible to predict based on anything you could have known last month. In this formulation, the theory is confirmed– our understanding of what’s going on is exactly correct– only if when regressing that product on anything known at t – 1 we always obtain an R-squared near zero.
This is actually a feature of a broad class of dynamic economic models, which posit that some economic agent– whether it be individual investors, firms, consumers, or the Fed– is trying to make the best decisions they can in an uncertain world. Such dynamic optimization problems always have the implication that some feature of the data– namely, the deviation between what actually happens and what the decision-maker intended– should be impossible to predict if the decision-maker is behaving rationally. For example, if everybody knew that a recession is coming 6 months down the road, the Fed should be more expansionary today in hopes of averting the recession. The implication is that when recessions do occur, they should catch the Fed and everyone else by surprise.
It’s very helpful to look critically at which magnitudes we can predict and which we can’t, and at whether that predictability or lack of predictability is consistent with our economic understanding of what is going on. But if what you think you learned in your statistics class was that you should always judge how good a model is by looking at the R-squared of a regression, then I hope that today you learned something new.
I already loved this post from introduction..so i did not read but fully agree regression analyses is like monkeys typing to get Iliad.
Finance writer Mark Hulbert just ran with the “incredible correlation” of gold and Treasury yields based on 8 years of monthly observations.
http://www.marketwatch.com/story/the-incredible-gold-interest-rate-correlation-2014-01-22
great post – I work in financial markets and constantly see use/abuse of R-bar-squareds in regressions from people who should know better!
Those models aren’t the same at all. The second one has pt-1 on both left and right side. The first has pt-1 only on the left side.
“I already loved this post from introduction..so i did not read but fully agree regression analyses is like monkeys typing to get Iliad.”
…and odds are some of those monkeys are going to get “laid” before they get “Iliad”?
JDH Well done. I never understood the R-square fetish that so many people have. It’s hard to believe that they picked it up from any econometrics class or textbook because almost every author screams about the hazards of looking too closely at the R-square. Like I said in another post, back in the day when I took econometrics we were taught not to pray to that god.
Of what use is a model that assumes all trading agents use the same valuation reasoning (“rationality”) with the same symmetrical information?
But neither series is linear as shown.
So you’d have to transform the data any ways?
I don’t really see what general point is being made here.
Typically the point is the opposite that even if an r2 is low if it has a high p value it may still be very informative. In your examples the whole thing is just wrong never mind the r2 no?
Nate: I know the equations look different, and they summarize regressions that you would run with different commands. But the predictions for pt that come from the two regressions, and the errors of those predictions, are going to be exactly the same number to the fifth decimal point.
dan: Sure, it would be better to take logs first, but I didn’t want to distract people with that, and the broad results would be the same. The main point I was trying to make is that you can drastically change the R-squared without making any changes in the model. So you can’t use the R-squared to decide if the model is good or bad.
This is a good post — but I would note that the R2’s are different because your regression equations are telling you different things, not because R2 is bad.
Both of the first equations say that AR(p) processes are good descriptions of the time series in levels, but basically useless in differences.
I’m not sure that’s a fault of the R2 so much as a responsibility to know where the predictiveness of the econometric model is coming from.
Professor Hamilton,
Is it worth your time to talk a bit about non-stationary and stationary time series? The level of the S&P being an example of a non-stationary time series and the 1st difference of the level time series being an example of perhaps a stationary time series.
I think you get mixed up in your own distinctions here, for instance: “That’s not a bad empirical description of stock prices– nobody can really predict them.”
This is FALSE. You’ve just shown that stock PRICES are tremendously predictable – take something like yesterday’s price, and today’s will be quite similar. Stock CHANGES are not predictable.
I agree with the overall point of the post, but my takeaway is “be careful that the model is describing what you want to predict” (level vs change) – a point which you get confused about yourself!
Yes, this is a very common fallacy. It’s great that your are pointing it out.
Another example that makes the same point is an estimation of the old Keynesian consumption function. Suppose we estimate
C(t) = a + bY(t) + u(t)
Then, we decide to estimate the Keynesian savings function instead where S(t) = Y(t) – C(t) as
S(t) = a + bY(t) + u(t)
These models are exactly the same. And yet you’ll get a higher R^2 from the consumption function estimation than you’ll get from the savings function estimation.
There’s a good trick you can use to exploit this fallacy. Let’s say that there is a model you want to defend to someone of who believes a high R^2 is necessarily good. Suppose when you estimate the model, you find a very large intercept term. Just drop the intercept term. Then re-estimate and measure R^2 as SSR/SST (regression sum of squares/total sums of squares). That will raise your R^2 big time. In fact, if the data cooperates it’s possible that will be able to say with pride to the unsuspecting: “My model is so good my R^2 is greater than 100%!”
On the other hand, if you want to knock down the model, do the same as above but measure R^2 as 1-SSE/SST, where SSE is sum of squared residuals. You can get a pretty low R^2 that way. And, as a bonus, if the data cooperates, you might be able to say: “This model is worse than useless. Why, your R^2 is negative!”
OT: Capex compression
Hess announced today its 2014 capital and exploratory budget.
Here it is, with the last two years’ data:
2014 budget: $5.8 bn
2013 budget: $6.8 bn
2012 budget: $8.3 bn
That’s a decline of 15% from last year, 30% from two years ago. Capex compression writ large.
Now imagine what’s going to happen to Shell’s budget.
My humble submission would be not to ignore the test for collinearity, that which would render high R square values meaningless and predictability therefore would be very weak. This is all the more reason why application of regression has limited role in most of areas that we use them in economics.
Is this not just due to the fact that stock prices and interest rates are integrated? Would this be a problem if the dependent variable were stationary?
AS and James: The issue I raise is certainly related to stationarity, but is not exclusively that. My second example (interest rates) is intended to illustrate that a similar issue arises in a stationary series with high serial correlation, with the well-known issues of the R-squared in a nonstationary regression being in some ways an extreme version of the consequences of very high serial correlation on a stationary series.
Other issues in a regression with nonstationary series such as (1) and (2) which I did not mention include the fact that the t-test of the null hypothesis that the lagged coefficient in (1) is unity (which is numerically identical to the t-test of the null hypothesis that the lagged coefficient in (2) is zero) does not have a standard Normal distribution, even asymptotically. Furthermore, we know from econometric theory that in the case of a nonstationary random walk, the R-squared from regression (1) goes to unity as the sample size goes to infinity, whereas the R-squared from regression (2) goes to zero.
Professor Hamilton,
Thanks. I always appreciate your comments.
Regarding the 10-year treasury rate (rate), I notice that using monthly data from 1990 to 2013, a model using (0,1,1) or using Eviews conventions, d(rate) MA(1) seems to have some predictive ability. Any comments would be appreciated if again worth your time for the blog.
How about you take the S&P, like
http://www.stern.nyu.edu/~adamodar/pc/datasets/histretSP.xls
add the dividends, subtract taxes on them and inflation, and do a log plot / fit ?
You might actually learn something from it.
1. I am aware that you might be pretty interested in my email. So be it, in the future, see below
I would like it very much, if you would add to your form, like most others blog owners, that you will neither share nor publish it. I would consider that very poor form. Just saying, nothing more implicated!
This time I give you the valid email of Paul Krugman, just to make sure, that your new setup doesnt disclose it, and waiting for the adding of the disclaimer,
2. I downloaded your 10-yr interest rate data, and confirm the fit parameters with the following data
0.00030 (please notice the missing Zero in your typing of the first parameter)
1.3701
-0.5887
0.2136
3. I implemented my own first multi variable, non linear analysis package 28 years ago, in FORTRAN at this time, from scratch
I can do sophisticated non-normal distribution data analysis at a level beyond commercial, industrial packages
In order for people understanding robust data analysis, let us take the data until end of 2008:
0.00037
1.3753
-0.5999
0.2189
0.00433
The first 4 numbers should be recognizable as close to the parameters above, the last number is the residual in a MS Excel Solver fit, very, very roughly R^2 = 1 – 2 x that is, in this context (please notice the multiple caveats, and my efforts to make this easily traceable in a very simple form for people who do not own commercial packages, and who know very little about statistics)
The subsequent development (with the monthly predicted values taken as an input) doesn’t cut it exactly
Date real prediction
2013-12-01 2.90% 4.87%
2013-11-01 2.72% 4.86%
2013-10-01 2.62% 4.85%
2013-09-01 2.81% 4.84%
2013-08-01 2.74% 4.83%
2013-07-01 2.58% 4.81%
2013-06-01 2.30% 4.80%
2013-05-01 1.93% 4.79%
2013-04-01 1.76% 4.78%
2013-03-01 1.96% 4.77%
2013-02-01 1.98% 4.76%
2013-01-01 1.91% 4.74%
2012-12-01 1.72% 4.73%
2012-11-01 1.65% 4.72%
2012-10-01 1.75% 4.71%
2012-09-01 1.72% 4.69%
2012-08-01 1.68% 4.68%
2012-07-01 1.53% 4.67%
2012-06-01 1.62% 4.66%
2012-05-01 1.80% 4.64%
2012-04-01 2.05% 4.63%
2012-03-01 2.17% 4.62%
2012-02-01 1.97% 4.61%
2012-01-01 1.97% 4.59%
2011-12-01 1.98% 4.58%
2011-11-01 2.01% 4.57%
2011-10-01 2.15% 4.55%
2011-09-01 1.98% 4.54%
2011-08-01 2.30% 4.53%
2011-07-01 3.00% 4.51%
2011-06-01 3.00% 4.50%
2011-05-01 3.17% 4.48%
2011-04-01 3.46% 4.47%
2011-03-01 3.41% 4.46%
2011-02-01 3.58% 4.44%
2011-01-01 3.39% 4.43%
2010-12-01 3.29% 4.41%
2010-11-01 2.76% 4.40%
2010-10-01 2.54% 4.39%
2010-09-01 2.65% 4.37%
2010-08-01 2.70% 4.36%
2010-07-01 3.01% 4.34%
2010-06-01 3.20% 4.33%
2010-05-01 3.42% 4.31%
2010-04-01 3.85% 4.30%
2010-03-01 3.73% 4.28%
2010-02-01 3.69% 4.27%
2010-01-01 3.73% 4.25%
2009-12-01 3.59% 4.24%
2009-11-01 3.40% 4.22%
2009-10-01 3.39% 4.20%
2009-09-01 3.40% 4.19%
2009-08-01 3.59% 4.17%
2009-07-01 3.56% 4.16%
2009-06-01 3.72% 4.14%
2009-05-01 3.29% 4.12%
2009-04-01 2.93% 4.10%
2009-03-01 2.82% 4.09%
2009-02-01 2.87% 4.08%
2009-01-01 2.52% 4.10%
2008-12-01 2.42% 4.08%
2008-11-01 3.53% 3.91%
2008-10-01 3.81% 3.66%
2008-09-01 3.69% 3.88%
2008-08-01 3.89% 3.94%
Why? Because that is not some simple physical differential equation game, but political, The Fed does it, via QE
Isn’t the high R^2 just saying last month’s price incorporates almost all the information available at the time for predicting this month’s price (other variables don’t matter a lot), while the low R^2 in price differences tells us last month’s prices gives us no information about the direction or magnitude of the price change?
Professor Hamilton and others on this thread might be interested in my post http://businessforecastblog.com/predicting-the-sp-500-or-the-spy-exchange-traded-fund/
Basically, I have incontrovertible evidence, checked and re-checked, that low power regressions can, in fact, produce trading profits for the SPDR SPY exchange traded fund which of course tracks the S&P 500. My guess is that there is a huge error here in the conventional wisdom related to imagining that the distribution of daily returns is anywhere remotely near Gaussian, and that residuals of equations such as discussed in this post, also are profoundly non-normal probably. I think I understand how the special characteristics of these distributions supports prediction in this context, with a simple strategy. My period of analysis is post-2008, incidentally, and I suspect QE has something to do with the success of these types of programs. I welcome feedback.