A common problem in economics is that most of the variables we study have trends. Even the simplest statistics like the mean and variance aren’t meaningful descriptions of such variables. One popular approach is to remove the trend using the Hodrick-Prescott filter. I’ve just finished a new research paper highlighting the problems with this approach and suggesting what I believe is a better alternative.
The Hodrick-Prescott filter can be motivated as choosing a trend that is as close as possible to the observed series with a strong penalty for changing the trend too quickly. The typical value for the penalty parameter used for analyzing quarterly data is 1600. I show in my paper that for an observation at some date t near the middle of a large sample, the deviation from trend (denoted ct) that emerges from this procedure can be characterized as
[math]!
c_{t}=89.7206\times \{-\Delta ^{4}y_{t+2}+\sum\nolimits_{j=0}^{\infty
}(0.894116)^{j}[\cos (0.111687j)+8.9164\sin (0.111687j)]q_{t}^{(j)}\}
[/math]
[math]!q_{t}^{(j)}=\Delta ^{4}y_{t+2-j}-0.78951\Delta ^{4}y_{t+1-j}+\Delta
^{4}y_{t+2+j}-0.78951\Delta ^{4}y_{t+3+j}
[/math]
Here [math]\Delta^4[/math] denotes the fourth difference– the change in the change in the change in the change. Maybe the growth rate (the first difference) has some trend, and maybe even the change in the growth rate (the second difference) has a trend too, but by the time we get to a fourth difference we’ve presumably taken all the trends out. All the other terms in the above expression put a lot of smoothness back in, but without any trends.
Is this a sensible procedure to apply to economic time series? The leading case we should consider is a random walk, which is a series for which the first difference (the change in the variable) is completely unpredictable. As I note in the paper [slightly rephrased]:
Simple economic theory suggests that variables such as stock prices (Fama, 1965), futures prices (Samuelson, 1965), long-term interest rates (Sargent, 1976; Pesando, 1979), oil prices (Hamilton, 2009), consumption spending (Hall, 1978), inflation, tax rates, and money supply growth rates (Mankiw, 1987) should all behave like random walks. To be sure, hundreds of studies have claimed to be able to predict the changes in these variables. Even so, a random walk is often extremely hard to beat in out-of-sample forecasting comparisons, as has been found for example by Meese and Rogoff (1983) and Cheung, Chinn, and Pascual (2005) for exchange rates, Flood and Rose (2010) for stock prices, Atkeson and Ohanian (2001) for inflation, or Balcilar, et al. (2015) for GDP, among many others. Certainly if we are not comfortable with the consequences of applying the Hodrick-Prescott filter to a random walk, then we should not be using it as an all-purpose approach to economic time series.
It’s easy to see what happens when you apply the filter to a random walk. As noted by Cogley and Nason (1995), if we only need one difference to produce something completely unpredictable ([math]\Delta y_t = e_t[/math]), then the other three differences plus all the other terms are simply adding all kinds of dynamics that have nothing to do with how the data really behave:
[math]!c_{t}=89.7206\times \{-\Delta ^{3}e_{t+2}+\sum\nolimits_{j=0}^{\infty
}(0.894116)^{j}[\cos (0.111687j)+8.9164\sin (0.111687j)]q_{t}^{(j)}\}
[/math]
[math]!q_{t}^{(j)}=\Delta ^{3}e_{t+2-j}-0.78951\Delta ^{3}e_{t+1-j}+\Delta
^{3}e_{t+2+j}-0.78951\Delta ^{3}e_{t+3+j}
[/math]
For example, the top left panel in the figure below shows the correlation between the change in the log of stock prices in quarter t and the change j quarters earlier. The top right panel does the same for changes in the log of consumption. As expected from the studies mentioned above, there is little evidence that you can predict changes in either of these variables from its own lagged values, or from lagged changes in the other variable (bottom panels), consistent with a random walk.
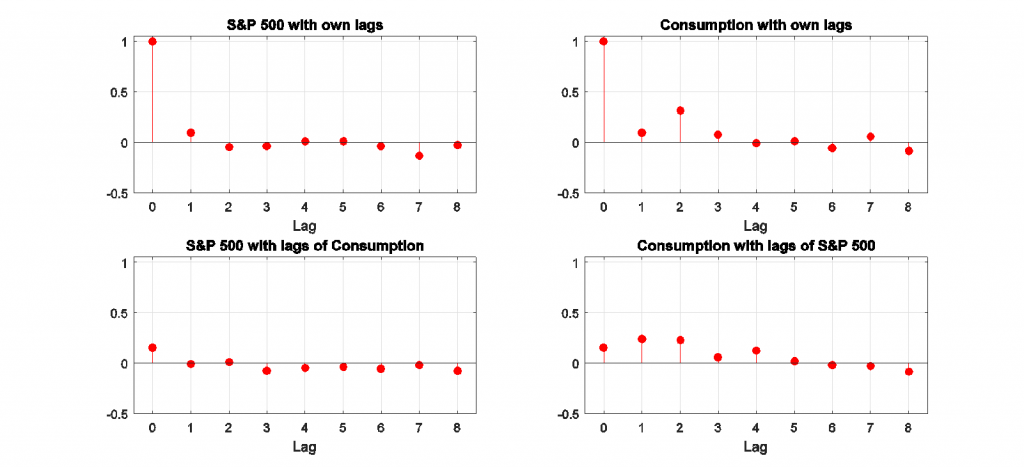
Autocorrelations and cross-correlations for first-difference of stock prices and real consumption spending. Source: Hamilton (2016).
By contrast, here’s what the correlations look like for HP-detrended stock prices and consumption. As I note in the paper:
The rich dynamics in these series are purely an artifact of the filter itself and tell us nothing about the underlying data-generating process. Filtering takes us from the very clean understanding of the true properties of these series that we can easily see in the first figure to the artificial set of relations that appear in the second. The values plotted in the second figure summarize the filter, not the data.
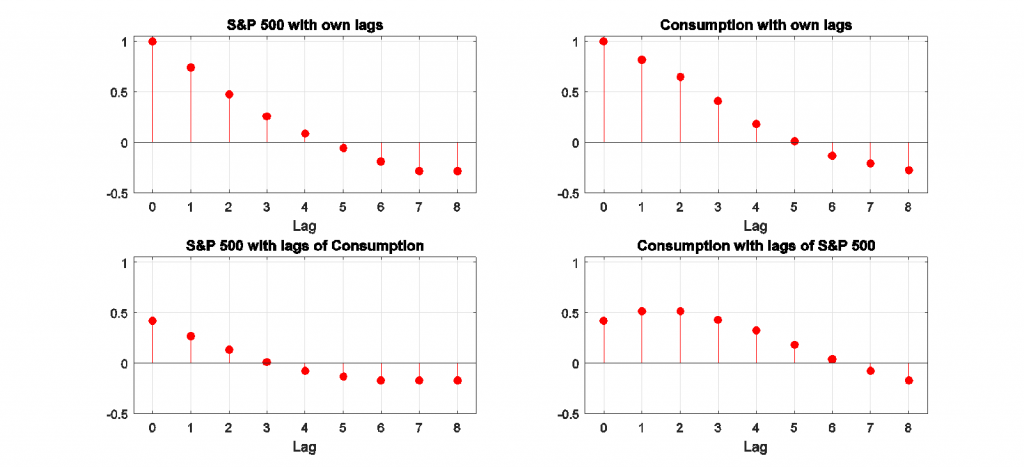
Autocorrelations and cross-correlations for HP-detrended stock prices and real consumption spending Source: Hamilton (2016).
There is one rather special case for which the HP filter is known to be optimal, which is if the second difference of the trend and the difference between the observed variable and its trend are both impossible to forecast. However, I show in my paper that if you took that specification seriously, you could estimate from the data the value for the smoothing parameter that would be consistent with the observed data. I found that when I did this for a dozen common economic variables, the implied value for the smoothing parameter is around one, which is three orders of magnitude smaller than the value of 1600 that everyone uses.
But the real contribution of my paper is to suggest that there’s a better way to do all this. I propose that we should define the trend as the component that we could predict two years in advance, and the cyclical component as the error associated with that two-year-ahead forecast. But don’t you need to know the nature of the trend in order to form this forecast? The surprising answer is no, you don’t.
The basic insight is that if [math]\Delta^d y_t[/math] is stationary for some value of d, then you can write the value of the variable at date t + h as a linear function of the d most recent values of y as of date t plus something that is stationary. If you do a simple regression of yt+h on a constant on the d most recent values of y as of date t, the regression will end up estimating that linear function. The reason is that for those coefficients the residuals are stationary, while for any other coefficients the residuals would be nonstationary. Choosing coefficients to minimize the sum of squared residuals (which is what regression does) will try to find the coefficients that take out the trend, whatever it might be.
But what if we don’t know the true value of d? That’s again no problem. If we regress yt+h on a constant and the p most recent values of y as of date t for any p > d, , then d of the estimated coefficients will be used to uncover the trend and the other coefficients will help with forecasting the stationary component. If we use p = 4, we have the same flexibility of the HP filter (it can remove the trend even if we need 4 differences to do so), but without all the problems.
In the case of a random walk, we know analytically what this calculation would be. If the change is unpredictable, then the error you make predicting the variable h quarters ahead is just the sum of the changes over those h quarters. The easy way to calculate that sum is to just take the difference between yt+h and yt.
The figure below illustrates how this works for nonfarm payroll employment. The raw data are plotted in the top panel, and the cyclical or detrended component is in the bottom panel. I calculated the latter using both the residuals from a regression of yt+8 on a constant and yt, yt-1, yt-2, yt-3 (shown in black) and using just the sum of the changes between date t and t+8 (in red). The latter two series behave very similarly, as I have found to be the case for most of the economic variables I have looked at.
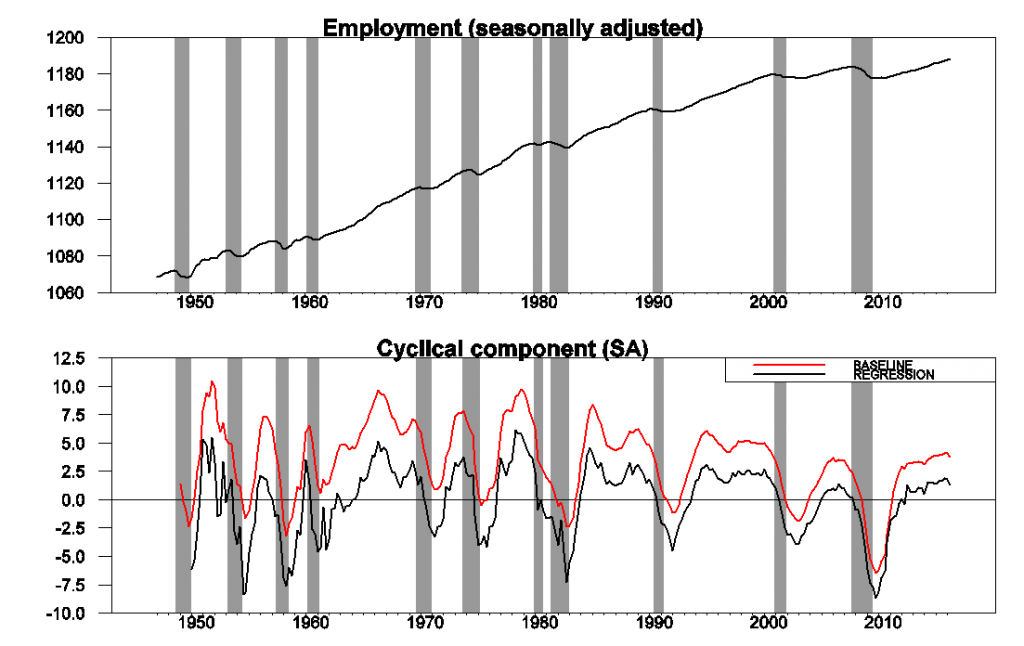
Upper panel: 100 times the log of end-of-quarter values for seasonally adjusted nonfarm payrolls. Bottom panel: residuals from a regression of yt+8 on a constant and yt, yt-1, yt-2, yt-3 (in black) and value of yt+8 – yt (in red). Shaded regions represent NBER recession dates. Source: Hamilton (2016).
One interesting observation is that the cyclical component of employment starts to decline significantly before the NBER business cycle peak for essentially every recession. Note that, unlike patterns one might see in HP-filtered data, this is summarizing a true feature of the data and is not an artifact of any forward-looking aspect of the filter.
Another benefit of this approach is that it will take out the seasonal component along with the trend. For example, the next figure shows the effects of applying the identical procedure to seasonally unadjusted employment data. The raw data (top panel) have a very striking seasonal component, whereas the estimated cyclical component (bottom panel) is practically identical to that derived from seasonally unadjusted data.
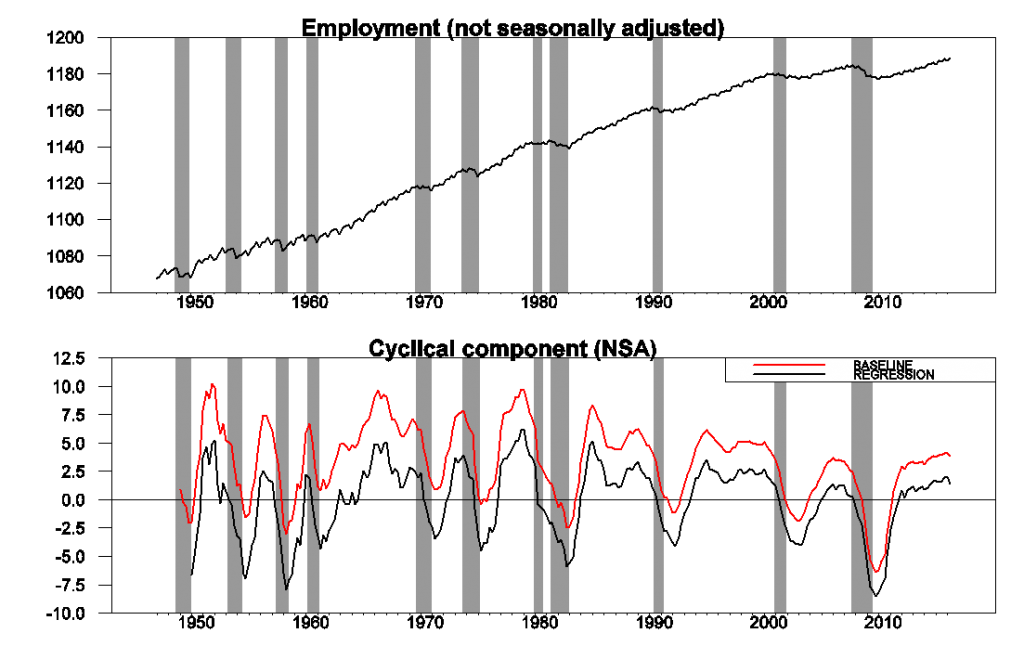
Source: Hamilton (2016).
The following graphs show the detrended behavior of the main components of U.S. real GDP. As I note in the paper,
Investment spending is more cyclically volatile than GDP, while consumption spending is less so. Imports fall significantly during recessions, reflecting lower spending by U.S. residents on imported goods, and exports substantially less so, reflecting the fact that international downturns are often decoupled from those in the U.S. Detrended government spending is dominated by war-related expenditures– the Korean War in the early 1950s, the Vietnam War in the 1970s, and the Reagan military build-up in the 1980s.
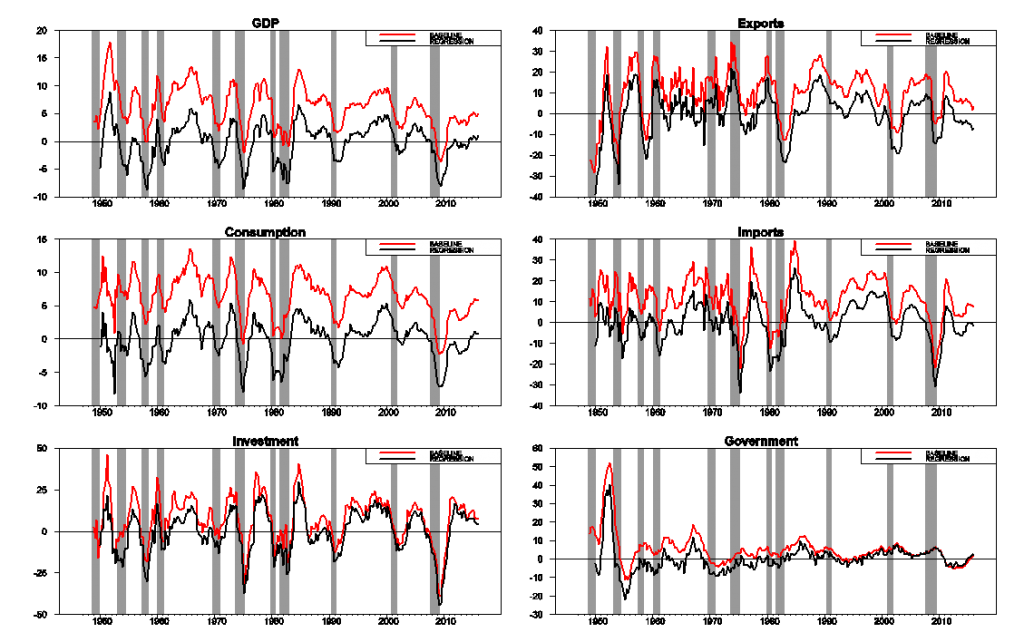
Source: Hamilton (2016).
Here’s a slight rephrasing of the paper’s conclusion:
The HP filter will extract a stationary component from a series whose fourth difference is stationary, but at a great cost. It introduces spurious dynamic relations that are purely an artifact of the filter and have no basis in the true data-generating process, and there exists no plausible data-generating process for which common popular practice would provide an optimal decomposition into trend and cycle. There is an alternative approach that can also isolate a stationary component from any series whose fourth difference is stationary but that preserves the underlying dynamic relations and consistently estimates well defined population characteristics for a broad class of possible data-generating processes.
Great article. Some interesting points!
Thanks
Professor Hamilton,
While trying to duplicate your example, and inserting recession bars from EViews and overlaying FRED series USRECM(to confirm the EViews placement), my recession bars seem to be shifted a bit to the right compared to yours, resulting in the curves showing more advanced warning of recession. What am I missing?
AS: The value of yt+8 – yt on the vertical axis should be lined up with date t+8 on the horizontal axis. Data and RATS code to produce figures here.
Thanks. It’s a privilege to interact with you and Professor Chinn.
Why two years?
MM: Using a multiple of 4 for quarterly data or 12 for monthly data is what allows the filter to remove seasonal factors along with the trend. The series can be interpreted as a forecast error, and I maintain that the primary reason a 2-year-ahead forecast will be wrong is if you miss the next recession or underestimate the strength of the boom. Finally, in many theoretical models, the shocks have mostly died down after two years, so that the two-year-ahead forecast corresponds to the steady state of the model. Even if it does not, you can calculate the two-year-ahead forecast error in your stationary theoretical model, compare it with the two-year-ahead forecast error in the nonstationary data, and we are making an apples-to-apples comparison for thinking about relating model to the data in the spirit that Prescott originally intended, but which the HP filter itself fails to deliver.
Professor Hamilton,
” I propose that we should define the trend as the component that we could predict two years in advance, and the cyclical component as the error associated with that two-year-ahead forecast. ”
Would you consider expanding on the above statement, perhaps showing how you would forecast PAYEMS using the proposal above?
AS: The 2-year-ahead forecast as of date t is the fitted value from a regression of yt+8 on a constant and yt,yt-1,yt-2,yt-3
Thanks. If I am doing this correctly, the coefficients on y(-2) and y(-3) do not seem to be statistically significant. Also, it seems that the residuals to the model are correlated. Again, if my calculations are correct, do these mentioned issues cause any concern?
AS:Typically (in what I refer to as the baseline case on page 17 as the baseline version of the approach) we expect those coefficients to be zero. And the errors are certainly expected to be serially correlated, which is completely consistent with the assumptions in the proof of proposition 4 in the paper.
Thanks,
However, I think I need one of your Econbrowser translations to fully appreciate the above comments and to fully appreciate your paper.
For the GDP and components comparison, the appropriately weighted component trends must add up to the GDP trend. Since everything is linear, do the weights fall out of your procedure? Alternatively, since your procedure is interpreting the cycle as forecast errors, can you get a propagation of errors comparing components to aggregates? Thoughts on a VAR extension or comparison to / re-interpretation of multivariate methods, i.e. Stock-Watson dynamic factor model?
Tom: The average value of the trend as calculated by my method is by construction exactly equal to the average value of the series. If some linear combination of any set of variables is equal to some aggregate variable, then the average linear combination of the trends in those variables will exactly equal the average trend in the aggreate.
One complication though is that I recommend using logs, and the sum of the logs of the individual components of GDP does not equal the log of GDP. However, I would not expect this to make a lot of difference for calculations like these.
I don’t think there is a strong benefit to doing this in a multivariate setting. A univariate regression is sufficient to take out the trend, and if it’s really the case that a set of variables have a common trend, this is a way to let the data speak for themselves without imposing some theory. Remember that the HP filter is also a univariate method.
Professor,
Any thoughts on the band-pass filtering techniques versus your new approach? After all when viewed in finite samples and the frequency domain the widely used CF filter is also a one-sided approximation at the end of the sample. So the same problem as in the case of the HP arises. One more thing. Did you try to check the real-time properties of your new method? It would be interesting to see if it outperforms other commonly used filters. Since Orphanides and van Norden paper we know this task is tricky.
Thanks for this paper, it is good to see that time series econometrics is still in play.
Best,
Pawel
I tried this method with Russian GDP data and it gives somewhat funny results: OLS coefficient for lag 3 is negative and for lag 4 is positive, which creates a strange twist: https://github.com/DanielShestakov/filters_example/blob/master/HamFilter.pdf
Could it be that I need to do constrained OLS with positive coefficients?
(I posted R code also: https://github.com/DanielShestakov/filters_example/blob/master/HamiltonFilter.R)
Daniel,
In the regression you use lags 1 to 4 of GDP. If I understood Prof. Hamilton correctly, you should use lags 0 to 3.
Terrific paper.
Although I never worked with an HP filter, I always regarded it with some scepticism as it appeared to present empirical economists with too many arbitrary choices and thus I suspected that it was conducive to rent seeking behaviour in the form of creative data mining.
Minor quibble: This paper applies to macroeconomic series. Not ‘economic time series’. If I am incorrect and the paper does apply to microeconomic time series then it is critical to include examples of microeconomic time series.
Why wouldn’t one just use a Dickey-Fuller test and take differences here?
One very common task in finance and economics is to calculate the underlying trend of a time series. This is a well-known problem in communication systems, and it is accomplished by designing a low-pass filter: a filter that eliminates high-frequency components of an input. For hard-to-understand reasons, some economists use the Hodrick-Prescott Filter (the “HP Filter”) as a low-pass filter. Unfortunately, the HP Filter violates several principles of filter design, and generates misleading output. As a result, it should never be used. Although this topic sounds fairly technical, problems can be easily illustrated graphically. Even if you are not interested in filtering series yourself, these problems must be kept in mind when looking at economists’ research if it is based upon the use of this filter. The conclusions may be based on defects created by the filtering technique.