I’m just finishing writing a new research paper whose goal is to come up with a better measure and understanding of the lagged effect of monetary policy on the economy. One of my claims is that the public’s expectations of what the Fed is going to do next play a key role in that process. In this, the first of several posts based on that paper, I describe some of the properties I’ve found for fed funds futures prices as predictors of subsequent Fed policy changes.
The primary policy tool of the U.S. Federal Reserve is manipulation of the federal funds rate, an overnight interest rate on interbank loans that is quite sensitive to the total quantity of reserve deposits that are created by the Fed. The Chicago Board of Trade offers a futures contract whose payoff is based on the average value for the effective fed funds rate over all of the calendar days of a specified month.
If this were a pure forward contract, no money would change hands until the first-of-month settlement day. The actual futures contracts are a little more complicated, since the exchange will require you to commit collateral to prove you can honor the contract, and these margin requirements will increase if the market moves against you. However, a recent paper by Monika Piazzesi and Eric Swanson demonstrates that the impact of these margin calculations on the value of the contracts should be quite small, and I will discuss here the simpler case of how to evaluate a pure forward contract.
Consider first how a contract that specified a 5.25% value for the current month’s fed funds rate would be valued at the start of the last day of the month (the day before settlement). If the actual rate turns out to be lower than 5.25%, the next day the seller of the contract will have to compensate the buyer for the difference (paying $41.67 per basis point in the standard contract). If you were the buyer of the contract, this would for you be a pure profit. The primary consideration that might prevent you from taking this bet is a concern that perhaps the rate would end up above 5.25%, in which case you’ll owe money. If speculators are risk neutral, the contract price will be bid up or down to the point at which its implied interest rate just equals traders’ expectations of what the settlement rate will turn out to be.
On the next-to-last day of the month, similar logic would again imply that the price reflects the market expectation at that time. New information could well come in after this, causing the price to move up or down before settlement. But if it were possible to anticipate, say, a price increase between the penultimate and last day of the month, there is a pure profit opportunity from buying on October 30 and selling on October 31. A statistical principle known as the Law of Iterated Expectations implies that the October 30 price should not only equal the expected settlement value, it should also equal the expected October 31 price. As time goes on and new information comes in, of course we know that the price is likely to change. But none of us can predict the direction. In other words, this simple theory suggests that the futures price should follow a martingale, in which the best forecast of where the price is going to be tomorrow is always just today’s price.
In my statistical analysis I looked at daily changes in the interest rate implied by the current month’s fed funds contract (denoted f1d), the following month’s contract (f2d), and the month after that (f3d); for example, for d = October 31 we could consider the change in the October contract (f1d), the November contract (f2d), or the December contract (f3d). The graph below plots daily changes in the interest rate implied by the current month contract from October 1988 through June 2006.
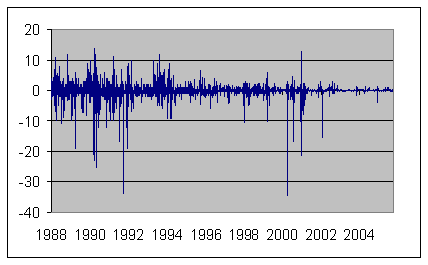 |
On average, the values of f1d, f2d, and f3d all turn out to be negative over this sample period, with t-statistics around -4. This represents strong evidence against the martingale hypothesis, and some researchers have interpreted this bias as evidence of some kind of average risk or hedging premium reflected in the futures prices.
However, if you look at the graph above, you will see that it is a pretty wild series. Forty-six percent of the observations are identically zero, while 25 observations exceed 5 standard deviations. The variance is considerably larger at the beginning of the sample or the start of a month, with the volatility appearing in clusters and particularly on days of major monetary policy announcements. If one models all these volatility dynamics and departures from a Gaussian distribution, the maximum likelihood estimate of the population mean of f1d, f2d, or f3d all turn out to be positive rather than negative, and far from statistically significant. The sample median of all three series is also exactly zero. I therefore see the nonzero sample mean not as an indication of bias on the part of futures markets, but rather as reflecting the fact that there were a few big moves down in interest rates over this period
that caught traders by surprise.
I also looked for whether changes could be predicted on the basis of lagged changes, by regressing fid on a constant and five of its own lagged changes. OLS coefficient estimates along with their 95% confidence intervals are shown below.
 |
The first lag is always highly statistically significant. Its value, however, is only around 0.15, which gives the regression an R2 of less than 0.03 and essentially zero predictability looking more than one day ahead. It is quite likely that this very modest degree of predictability could be attributed to measurement error in resolving daily bid-ask factors rather than systematic errors or risk factors in futures markets.
The paper by Piazzesi and Swanson mentioned above documents some predictability using monthly data of longer-horizon fed funds futures prices based on a number of interest rate spreads. However, consistent with their findings, I find these spreads do not predict the daily movements in the prices associated with the near-term fed funds futures contracts that I am studying, as summarized in the table below:
| Explanatory variable | Dependent variable | ||
|---|---|---|---|
| xd-1 | f1d | f2d | f3d |
| 10-year minus 5-year Treasury spread | 0.058 (0.086) | -0.036 (0.117) | -0.070 (0.138) |
| 5-year minus 2-year Treasury spread | -0.009 (0.058) | -0.085 (0.079) | -0.126 (0.093) |
| 2-year minus 1-year Treasury spread | -0.072 (0.112) | -0.136 (0.153) | -0.172 (0.181) |
| 1-year minus 6-month Treasury spread | 0.006 (0.173) | 0.302 (0.236) | 0.439 (0.279) |
| Baa minus 10-year Treasury spread | -0.035 (0.058) | -0.126 (0.079) | -0.184* (0.094) |
| 12-month job growth (revised data) | 0.017 (0.023) | 0.089** (0.031) | 0.125** (0.036) |
| 12-month job growth (real-time data) | 0.016 (0.024) | 0.093** (0.033) | 0.121** (0.039) |
I also replicate with these data Piazzesi and Swanson’s observation that employment growth helps predict futures prices, though again for my data the R2 is only 2%, and the results I will describe in my next post turn out to be insensitive to whether one includes this conditioning variable. Overall, I conclude that although these data do not appear to follow an exact martingale, that is really an excellent approximation to their behavior.
A separate question from whether changes in futures prices are possible to predict is the question of how far in advance they give a useful estimate. One standard of comparison is the mean squared error, or the average squared difference between the implied futures forecast at a given date and what the actual fed funds rate turns out to be. A benchmark for comparison is the assumption that the fed funds rate itself follows a martingale, so that one’s forecast for the future value of the fed funds rate is always its current value. Such “no-change” forecasts have often proven to be very difficult to beat out-of-sample with financial data. The table below shows that, if you simply predicted that the fed funds rate isn’t going to change, you’d have a mean squared error of 389 basis points (that is, a standard deviation of about 20 basis points or 0.2%) predicting one month ahead and 2,522 basis points (50 basis-point standard deviation) predicting 3-months ahead. For comparison, the MSEs of the futures-derived forecasts are only a third as large.
| Forecast horizon | No-change MSE | Futures MSE | Percent MSE improvement | Futures MAE |
|---|---|---|---|---|
| 1 month ahead | 389 | 128 | 67% | 6.90 |
| 2 months ahead | 1248 | 392 | 69% | 12.76 |
| 3 months ahead | 2522 | 914 | 64% | 20.03 |
Futures prices have become even better predictors over the last three years, with an incredible 97% improvement over the “no-change” forecast:
| Forecast horizon | No-change MSE | Futures MSE | Percent MSE improvement | Futures MAE |
|---|---|---|---|---|
| 1 month ahead | 183 | 5 | 97% | 1.50 |
| 2 months ahead | 665 | 19 | 97% | 3.18 |
| 3 months ahead | 1484 | 48 | 97% | 5.40 |
The moral is, if you think the fed funds rate is going to do something over the next few months that differs from what is predicted by the futures prices, then think again.
And what the futures prices say right now is, no change in November or December.
Technorati Tags: macroeconomics,
Federal Reserve,
futures markets,
interest rates,
fed funds rate
The front two contracts in Fed Funds and even the third now have become irrelevant..
In your data it would do to take care in obvserving the calendar date of the FOMC meeting..
The January contract currently has little or no volatility, its value is almost entirely a function of the December FOMC outcome..
February is the lead contract now.. as of yesterday.. it was the Fifth contract trading..
As Swanson and others at the FED have figured out.. its usually the properly calibrated “calendar spread” that provides the market assesment of the upcoming policy move..
And up until recently the entire enterprise has been made more complicated by the trinomial natutre of the possbilities.
The FED could possible.. Tighten, Stay on Hold, or EASE.. .
This makes the price of the futures alone insufficent, on has to have access to the FedFunds options marketplace to calibrate.
Sjonas, the December contract is only “irrelevant” if you are already persuaded there will be no target change at the Dec. 12 meeting. If you are so persuaded, you are on the correct side of the bet. At least that’s what futures say.
You are correct that an expected value of “no change” could in theory be consistent with a 30% probability of increase and a 30% probability of decrease. In practice, it almost never works that way.
My primary point was to investigate evidence for the martingale property, for which the FOMC dates are irrelevant.
As for why I’m using only the near-term contracts, if you study the Piazzesi-Swanson paper, you will see there are some problems with using the longer term contracts. Particularly in the early part of the sample, these were not so actively traded.
If what you want me to take from this article is that the predictive value of CBOT is what predicates the fed move, you’ll have to wait. I don’t believe this is what you want me to take from this article.
If what you want me to take from this article is that CBOT is valuably predictive of any given fed move, you’ll also have to wait. I don’t believe this is what you want me to take from this article, as you’re discussing an after the fact analysis of the correlation.
What the CBOT does is like what a bookie does, and nothing more. The CBOT covers losses by analysing where the money is being bet adjusting as its exposure in either direction unfolds by margin calls and adjusting margin rates.
What the fed does, is set rates.
What I think you want me to take from this article is that it’s not likely the data available will allow anyone to carefully manage their money and by placing a small percentage of their available capital in conservative bets in the futures market to live off the fat of the land, and, I believe this on average is certainly true. In the ideal, the odds are a slightly less than zero sum against this happeneing.
It’s true because CBOT has the data before anyone else, and it’s wholly a fluke when anyone makes a gain against the futures market by making their analysis through numbers put out after the fact of CBOT having them. They’re simply betting without having all the timely knowledge CBOT has.
And here, while it’s possible to think, and even show through statistical models that one can know what’s happening after the fact, as the instance of prediction approaches, it’s still almost like flipping a coin, if not in the fifty-fifty chance of flipping a coin.
However, even if heads come up three times in a row, or even eight times in a row, when flipping a coin the odds are still only fifty-fifty that the next flip will come up tails, and it’s just as likely it will come up heads. There’s the illusion you’re alluding to, unmasked in a very simplistic way.
This however, does not rule out those with large amounts of capital moving the futures market in a way to extract the suckers’ money that is being waged.
(Also, I believe a margin call rate adjustment can be made at any stage of the game in the futures market, which is neither well nor explicitely stated within your article.)
It would be nice, if everyone was brilliant enough and if the odds permitted it, and we could all play the futures market and never have to work, but this is not the nature of this game.
If it was the nature of the game, CBOT would be quickly out of business.
It would be nice if we could all buy lottery scratch tickets and come up with enough winners so that none of us would have to work too. But this is not the nature of that game either.
All these games are designed to take your money, so why anyone plays them is beyond me. It’s like walking around with a tatoo on your forehead that says, I THROW MY MONEY AWAY, BUT YOU’LL NEVER BE A WINNER IF YOU DON’T PLAY THE GAME.
I’m getting five percent in a FDIC backed money market fund, and, I get five percent on the interest that acrues too.
That’s the miracle of compound interest.
Of everthing I’ve said here in this post, the only thing that relates more than parenthetically to economics, is the immediately preceding sentence.
There are games set up in which you can win. And while during the first year, your money in the bank earning interest doesn’t keep up with inflation, the really too well kept secret is, it actually beats inflation every year there after if you keep it in the bank.
That’s a no brainer, and again, that’s the miracle of compound interest.
Don Robertson, The American Philosopher
Limestone, Maine
An Illustrated Philosophy Primer for Young Readers
Precious Life – Empirical Knowledge
The Grand Unifying Theory & The Theory of Time
http://www.geocities.com/donaldwrobertson/index.html
Art Auctions:
http://www.artbyus.com/auctions.php?a=6&b=4807
Profs…you earlier posted formulas written by clever fed researchers that estimate the probability of recession based on yield spreads.
are these formulas applicable to other federal government bond markets, specifically the UK, NZ and Australia bond markets, which all sport inverted 3 month 10 year spreads. Thank you.
I’d imagine the reason why the markets have done so much better than “no change” for the past three years is that the Fed has almost always changed! And in a very predictable way; for 18 months it raised one quarter percent every meeting. This predictability appeared to be one of its policy goals so it is not too surprising that the markets did much better than “no change” in this period.
Needless to say, the FOMC is paying attention to this market. We also know that they do not wish to disturb “the markets.” Hence, one would expect that there would be a certain tendency to do what this forward market says, requiring some rather strong, and perhaps inside information-based reasons, to do otherwise.
Sure they are paying attention. But they are in the caboose…
http://www.ltadvisors.net/Info/research/FedFollows.gif
No..
The methodology by which you derive the forecast of the futures price.. certainly that of the P&S paper is flawed..
Basically it takes an approximation, (that actually I developed one night at a bar) and runs with it..
The derived “rate” or probability of a FED move that is derived is only “accuarate” within a binomial framework.. where the potential policy actions of the central bank are “truncated” to either a 25 basis point move or nothing..
In reality, there are five states.. on hold, go 25, go 50 (i.e. more than 25), ease 25, ease more than 50..
The marketplace has long recognized this, and the sucesss of the FED FUNDS options, which in your way of thinking would be a totally redundant asset.. why have an option on an “binary” option to begin with…
As for December funds, they became interesting again. not because the FED is either going to go or not in December.. but .. they are beginning to price in (at least in the options marketplace) a small probability of the FED easing by the December FOMC..
Professionals in the marketplace use a vector notation {10,90,10} to discuss the probabiity embedded in any contract..
Puts reflecting the Feds’ possible tightening, and Calls reflecting a possible ease simultaneously trade.
Futures are nothing more than an ATM option and thus their price too embedds all possible probabiity paths..
Don’t be confused between a “martingale” and “expectations”.. here a good review of deFinetti’s work would be worth your while
Don Robertson’s comment below: Is perhaps the silliest I’ve seen from someone with Philospher in his title…
“However, even if heads come up three times in a row, or even eight times in a row, when flipping a coin the odds are still only fifty-fifty that the next flip will come up tails, and it’s just as likely it will come up heads. There’s the illusion you’re alluding to, unmasked in a very simplistic way.”
If heads come up eight times in a row?.. Why don’t we say. if the FED is in the midst of tightening 17 times…
If the coin is “biased” just like the Polya Urn.. it doesn’t take too much to figure out that the odds of the next draw (subjective odds) will change as 8 tails come up.. as in all probability it depends on your prior.. I suggest a re reading of Keynes here..
Anon-
Yes. I meant to be overly simplistic. It makes the point I meant to make, no one can know what the fed will do, except those to whom he gives the tip to, a tip concerning which he doesn’t later change his mind about, perhaps on his way to the rostrum?
So, if you’re going to get involved in this game that takes players’ money away a tad better than fifty percent of the time, and you think you have a crystal ball, I’d suggest you’d do much better to cozy up to the fed chairman, or someone he’s told which way he’s going to let the three-sided coin drop. You might even come out a winner, but you’re putting your chances at the mercy of a lie someone might stick you with.
Human nature is human nature though, and, I expect someone somewhere is today touting someone else’s amazingly unlikely win in the lottery too. You simply have to play to win! Yes, and to lose too.
The only thing I ever won in my entirely life, other than a few small sporting and even smaller academic events that were all on the up and up, was in 1962 when I was twelve years old. It was a beach association Halloween contest for the best costume, when my mother dressed me up as Aunt Jemima. I won that year. Wooo Hoooo!
I think the prize was an A.M. radio of some sort.
Put your money in the bank, and chase the banker at every turn of the month for a better rate of return. That’s my advice. Let someone else play those games of chance. It’s good advice too.
If you keep putting money in the bank, you may at some time in the future have enough, to find yourself fortunate enough, to end up at the right place at the right time, when having enough money can provide you with a reasonable, sound and secure business opportunity that carries no risk and a good rate of return for taking the unforeseen risks associated with business.
You still never want to put all your eggs in one basket, that’s simply a risk no one should take.
And, that’s why right now I worry about FDIC. It doesn’t keep me up at night like the futures market, or the advice of some ne’er-do-well concerning whatever, but I still wonder how secure FDIC is.
That’s the way a good business mind works.
Everyone else that “finally” gets lucky and ends up on top at some point, usually finds themself at the bottom again, though faster and far-far greater frequency.
Don Robertson, The American Philosopher
Charts, there is indeed international evidence on the the relation between an inverted yield curve and subsequent slower economic growth. However, I would not rely on the specific parameter values from Wright’s analysis of U.S. data and assume that those exact same parameter values would work for other countries as well.
Sjonas, you claim to have identified a flaw in the methodology by which I “derive the forecast of the futures price.”
I do not derive any forecast of the futures price. I read it directly off the CBOT database. The basic random variable whose properties I summarize is the daily change in this price.
Perhaps I have misled you by referring to the “no-change” forecast. I am using this as shorthand for the martingale property, which is that the conditional expectation of tomorrow’s value is equal to today’s. If the point you are making is that this is different from predicting zero variance, you are right. It of course is not true that zero expected change means zero probability of a Fed move. Zero expected change could be the result of a 20% chance of up and 20% chance of down.
Or perhaps you are focusing exclusively on the last sentence of the post, where I admit I am adding an interpretation to the current futures price that has implicitly made use of other information. But to infer from this that it is inappropriate to test the data for the martingale property is simply erroneous.
I do not know what you may have discovered in a bar that evening, but I do know that most Ph.D. economists learned the definitions of the conditional expectation of a time-series random variable and a martingale difference sequence from my book.
Thanks, professor (JDH).