There’s a lot of evidence of a rising inventory of unsold housing, and a big decline in housing sales. Can a more quantitative, stock-based figure be obtained?
This post is inspired by the questions from Matt and dgsullivan regarding my previous post which cited nominal housing stock figures. I was unsure of how the real housing stock figures fit into the the story of the housing downturn and hence thought a closer look was warranted.
One way of addressing the question is to rely upon a (not the) theory of housing investment. Let H[t] be the housing stock at time t, Y[t] be real GDP, and rH[t] be the real user cost of housing. Assume real output is a Cobb-Douglas function of housing capital (with exponent b) and other inputs. Then taking a partial differential of Y with respect to H yields the marginal product of housing, which in equilibrium should equal rH[t]. Those who know the the neoclassical theory of investment will see a familiar set of steps; whether this is the most appropriate manner in which to model the optimal residential housing stock, I leave to the reader. Re-arranging, one obtains:
H*[t] = bY[t]/rH[t]
The * denotes the equilibrium level. Using the real stock of housing and real GDP from BEA, and the real user cost of housing capital, proxied by the 10 year constant maturity Treasury rate (from FRED II) minus the survey-based 10 year ahead inflation rate (from the Society of Professional Forecasters), I obtain the following regression coefficient estimates:
h*[t] = 2.14 + 0.78(y[t]) – 1.25(rH[t])
where lowercase letters denote the log values. All coefficient estimates are statistically significant.
Using the estimates from the 1991-2005 period, one obtains the following fit in levels. The end 2005 predicted value was about 2 percent (in log terms) below the actual.
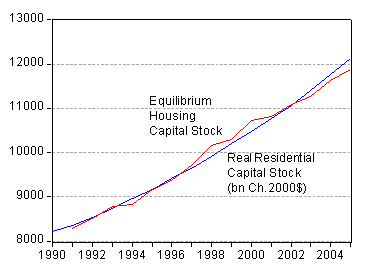
Figure 1: Actual and estimated equilibrium housing capital stock, in billions of Ch.2000$. Sources: BEA, FRED II, SPF via Philadelphia Fed, and author’s calculations.
With the end-2005 residential capital stock at 12.1 trillion Ch.2000$, this implies about a 242 billion Ch.2000$ overhang (not including whatever investment occurred in 2006). Since gross real residential investment in the first three quarters of 2006 is running at 784 billion Ch.2000$ per year, while depreciation is around 200 billion (the amount in 2004; 2005 was more, in part due to Katrina), the overhang is potentially 438+242 = 680 billion ch.2000$.
Another interesting aspect of the data is that the housing capital stock does not appear to move significantly in response to long-run disequilibria in this sample period; rather output and real rates seem to do much of the adjustment in a statistical sense. This result might be an outcome of the sample period, or the model selected.
Caveats: It’s not clear how reliable the statistical model is, given that we only have 15 years of data in the regression. Second, this is a completely neoclassical model, without any financial and informational frictions. Hence, this analysis should be taken as nothing more than a first cut, and certainly not to be taken as an alternative to flow-based analyses of residential sector investment.
Technorati Tags: housing,
residential capital stock,
residential investment, and
user cost of capital
Very interesting, Professor. Thank you.
I explored something similar, but in a different fashion: using current and historical Z-1s from the Federal Reserve, I plotted personal consumption, Federal consumption, and residential investment over ’46-’05. Federal consumption (16%) and residential investment (5%) seemed relatively level over the period. What was striking, to me, was the big increase in personal consumption: from 63% over ’46-’80 to 67% over ’81-’05. I calculated ‘overconsumption’ of $7.2T over ’81-’05, which inflated using the CPI to today was $9.9T.
Related, the increase in household credit market debt over that period was $10.0T.
To me, what really changed over ’81-’05 was a big reduction in savings. My question is, do we have to make up, now, for lost savings over ’81-’05? If yes, given modest productivity today, that’s a depression-level reduction in consumption ($10T over 5-10 years given our $13T GDP = ~8-15% reduction in GDP annually).
“Caveats: It’s not clear how reliable the statistical model is, given that we only have 15 years of data in the regression.”
It’s all in sample as well. It’s pretty easy to make any model look good in sample. The questions is how well it does out of sample.
Jeffrey Miller: Sometimes short samples are more problematic than other times. In particular, one would like to encompass more than one and a half cycles in order to assess trend phenomenon.
jg: You pose an interesting question. I don’t know if there is a “conservation of savings” sort of law in play. That is because relative prices change over time. But what is true is consumption was abnormally high (as a nominal share of GDP) over the past decade, and that needs to be validated by continued rapid productivity growth (or some manna from heaven — or at least overseas), in order for us not to have that non-saving be “made-up” with more saving in the future.
jg: An interesting point.
It dangerously reminds of Kondratiev’s theory and that it may still be fully valid these days. Even in the world of FIAT money.
If savings rate drops and consumption is done on debt in an increasing manner, according to the theory, it will eventually bring the relative price level up compared to relative wage level, at the end of the K-autumn the wages lag behind the real pricelevel. To my knowledge this has already happened since 1997.
The debt plays an increasing role to the end of the cycle, filling in the hole that relative pricelevel increase makes, but adds more debt to consumers. The debt level can increase and be maintained to a certain point, until the amount becomes overwhelming and cannot be supported anymore.
What makes the theory more interesting and I will point to the years 81 – 05 is that according to the theory, the interest rates decline through the K-autumn. That is exactly true since 1981 – 2005, interest rates have been declining on average exactly as the theory suggests. This can be explained by the debt level that rises through the same period, because the more debt there is the less interest rates the consumers overall can pay for. It also brings the inflation down, which is part of the theory as well. The more debt there is the more dominating effect interest rates will naturally have on the whole and thus will affect the inflation. So at the end the interest rates will finally, according to the theory, hit zero-bound.
Around that time the debt level maximum has been reached and can’t be supported anymore.
I’m just saying this out of interest, it would be interesting to know a professional comment whether this theory still today has some idea behind it, I think that alarmingly everything points to the fact that the end of K-autumn is coming fast. 1) Interest rates lowering 2) Debt levels going high up 3) Savings rate going down, now negative (this happened last time in 1932-1933, never in between, that is during Great Depression), 4) inflation going down all the way from the peak of 1980-1981, which was the turning point from K-summer to K-autumn, 5) wages lagging behind the pricelevel. 6) extreme confidence in stock and real-estate markets, ending in a possible bubble (at least real-estate market, but hard to see that that didn’t spill to stock markets as well), so far being supported by the increasing debt, now possibly bursting.
In last recession Fed took interest rates down to 1%. That time inverted yield curve occurred roughly one percent higher than it did now, are we going down very close to zero-bound this time, whenever the next recession happens?
I’ve been watching the housing market, and here are two factors I have noted are not showing up in any analysis, but which should be considered, as they throw off everything else.
1) The parents of the Boomers still own a significant percentage of the housing stock in this country. This demographic problem is accellerating because this class of owners is simply dying off at an exponentially rising rate. Just look around your neighborhood at the plus 75 crowd. All that real estate is coming on the market due to death attrition.
2) Property taxes are rising at rates much faster than even housing prices were rising before the downturn in housing. There comes a point where property tax costs will depreciate the value of every home. I mean, come on people! If your property taxes are higher than your cost to rent, what could be the incentive to achieve the American dream and buy into a declining market? This phenomenon is giving rise to a new class of what amounts to indentured servants, shackled to their plows, so to speak, by the deed to their home and a deficit in collateral versus debt.
If you still want to call that an investment, then, I’ve got a bridge in Brooklyn you might be interested in. Like the realtors say, At this price it won’t last long!
Don Robertson, The American Philosopher
Limestone, Maine
An Illustrated Philosophy Primer for Young Readers
Precious Life – Empirical Knowledge
The Grand Unifying Theory & The Theory of Time
http://www.geocities.com/donaldwrobertson/index.html
Menzie:
This seems very interesting, but I find the econo-jargon to be a formidable barrier.
I’m comfortable with the math and the economics concepts; but if you could give more details on the derivation (including what the inputs mean), I would be grateful.
In specific, what is the form of Y[t]? What is a “Cobb-Douglas function”? What is the real user cost of housing (something like OER)?
This blog could become an even better teaching tool if you explained things like this on a regular basis in the course of your discussions. Then outsiders like me could get a meaningful window on academic economics, and perhaps be able to contribute fresh insights.
For example, if I knew the details of what you were doing in this analysis, I could model the overhang based on alternative inflation metrics, such as M1, to see if it is better or worse than that based on the conventional data and reasoning.
Patriot: I don’t think this model necessarily is, or is not, related to Kondratieff waves. One would have to specify the set of imperfections or rigidities in order to produce the cycles predicted by Kondratieff.
Aaron Krowne: Sorry about that. The Cobb-Douglas function is one of, if not the, most common functional forms used in economics. So instead of the general functional form Y=f(H,N), one writes a parametric version Y = (H^sigma)x(N^[1-sigma]), where “^” means “taken to the power of”. Hence, X^2 is X squared. You’ll notice that the exponents sum to unity. Hence, Cobb-Douglas production functions exhibit constant returns to scale. The relevant reference is the same as what I cited in my post about the business investment handoff: Hall and Papell, Macroeconomics, the Investment chapter.