That’s the topic of my most recent research paper. Reader warning: this is a bit more technical than the standard Econbrowser post, so if you’re not a user of regression analysis, this may not be up your alley.
One of the contributions for which my colleague Rob Engle received the Nobel Memorial Prize in Economics was development of ARCH, a class of models for predicting the volatility of a variable. One’s first priority might be to predict the level of the variable, such as asking what the price of oil will be next month. With ARCH models, we instead try to predict the absolute or squared value of the change– are oil prices likely to change more this month than usual?
ARCH models have become popular in finance, where measuring the volatility is extremely important for purposes of characterizing the riskiness of portfolios. They have been less used by macroeconomists, who are usually interested in predicting how the levels of variables might change under different circumstances.
In my latest research paper,
I argue that even if one’s primary interest is in measuring consequences for the levels, it can be very important to use ARCH to model any changes in the volatility, for two reasons. First, correcting for outliers can give you much more accurate estimates of the parameters you’re interested in. Second, if you make no corrections, there is a possibility of a kind of spurious regression. The expression spurious regression is known to economists as a common finding when you regress two variables that have nothing in common except a tendency to drift from their starting values; (Jesus Gonzalo has some amusing examples). The result is high t statistics that would lead you to reject the null hypothesis of no relation, even though the null hypothesis is surely true.
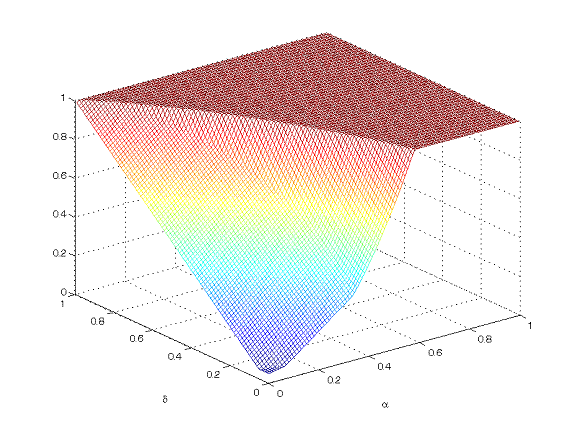
I found there’s a possibility of something similar arising if you rely on the usual OLS test of a hypothesis about a lagged dependent variable in a regression that is characterized by ARCH. If the sample size is large enough, you are certain to reject the null hypothesis that the coefficient is zero, even if the null hypothesis is true. For example, the diagram below shows the asymptotic probability you will reject a true null hypothesis of zero serial correlation as a function of the parameters α and δ of a GARCH(1,1) process for the residuals. This would be a flat plane at height 0.05 if the t test were doing what you expected, rejecting only 5% of the time when the null hypothesis is true. In fact, for α and δ in the range often found for macroeconomic series, you’d end up wrongly rejecting 100% of the time with the standard t statistic.
My paper also illustrates these issues with a couple of examples taken from the macroeconomics literature. The one I’ll discuss here involves estimation of the Taylor Rule, which is a description of how the Federal Reserve changes its target for the fed funds rate in response to variables such as inflation and GDP. The conventional understanding by most macroeconomists is that since 1979, the Fed has responded more aggressively to deviations of inflation or GDP from their desired levels, and that this change in policy has helped to stabilize the economy.
The first row in the table below reproduces that finding and its apparent statistical significance using OLS estimates of the coefficients and their standard errors. However, there is strong evidence of ARCH dynamics in the residuals of this regression. When one takes those into account in the estimation, the change in the responsiveness to inflation is 1/3 the OLS estimate, while the changed responsiveness to output is less than 1/10 of the magnitude one would have inferred by OLS.
| inflation | (std err) | output | (std err) | |
|---|---|---|---|---|
| OLS | 0.26 | (0.09) | 0.64 | (0.14) |
| GARCH | 0.09 | (0.04) | 0.05 | (0.07) |
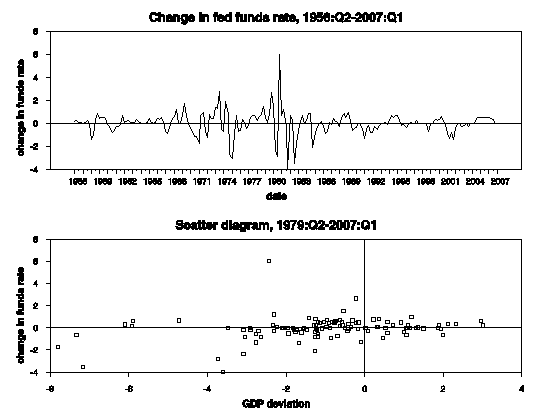
The diagram below displays the features of the data that are responsible for this result. The top panel is the monthly change in the fed funds rate, in which the ARCH features are quite apparent, with increased volatility particularly over the 1979-82 period. The bottom panel is the scatter diagram relating the change in the fed funds rate (vertical axis) to the output gap (horizontal axis) over the 1979-2007 subperiod. The apparent positive slope is strongly influenced by those observations for which the variability of interest rates is highest. Because GARCH downweights these observations for purposes of estimating the slope, the post-1979 response of the Federal Reserve to the output gap is significantly smaller than that estimated by OLS.
The recommendation that the paper offers for macroeconomic researchers is quite simple. It is extremely straightforward to test for the presence of ARCH effects– just look at the R2 of a regression of the squared residuals on their own lagged values. Macroeconomists might want to glance at this diagnostic statistic even if their primary interest is not the volatility but some other feature of the data.
Technorati Tags: macroeconomics,
ARCH,
GARCH,
spurious regression,
Taylor Rule
Interesting read. It has been a long time since I had to use statistics but, the gist I got was that the variables used in many macroeconomic models may not have as much explanatory power as thought or even none.
It also sounds like you are on top of the problem with tools to help in that regard.
“This would be a flat plane at height 0.05 if the t test were doing what you expected, rejecting only 5% of the time when the null hypothesis is true. In fact, for α and δ in the range often found for macroeconomic series, you’d end up wrongly rejecting 100% of the time with the standard t statistic.”
Can you expound on this? It would seem macroeconomists should do more than glance at this diagnostic statistic.
Hitchhiker, any statistic you use to test a particular hypothesis is designed to have a specified “size”, which refers to the probability that you would reject the null hypothesis even though it is in fact true. The graph shows the true size for a test that is supposed to have size 0.05. The null hypothesis is exactly true at every point on the graph. Thus, if the test statistic were designed correctly, the graph would be a flat plane at the height of 0.05. The fact that the graph is not a flat plane means that the test statistic is not performing correctly in the presence of ARCH. Specifically, if you think your test has size 5% (you are believing that it would only reject a true null hypothesis 5% of the time), but its actual size is 100% (in practice you will reject the null hypothesis every single time, even though it is in fact true), you have a real problem.
Regression is ever a perilous operation tho one powerful. What you seem to have here is a volatility error filter with a simple procedure. On the Niftyness Scale, JDH, that comes in at the kitchen microwave level, which is ‘significant.’ Congrats.
Your paper seems to use monthly changes in ffr, presumably the actual market ffr rather than the target. Or are you modeling the target, and hence only policy? After all, since last August there appears to have been a substantial increase in the daily (hence market, not policy) variations in the ffr, with it even going negative occasionally, if only briefly.
Jim,
Looked at your paper more closely. The technical argument certainly looks reasonable.
Regarding my last comment, at least during the high ffr volatility period of 79-82, well we know that this was the period of the “monetarist experiment,” even if Friedman and others have said that it was not a period during which what they would have recommended was being done precisely. But, in any case, the ffr was not the main policy target, even if there was a one set (I don’t know; was there?). But at the monthly level, if one was being set, presumably at the monthly level one would not observe any noticeable differences between target and market rates anyway. Those tend to occur at much higher frequency rates, e.g. daily.
So, in some sense bringing in ARCH is a way of getting at in a better way characterizing what the policy was during that period of high ffr volatility, which among other things, whether it was properly done monetarism or not, was not a period in which stabilizing or focusing upon the ffr was what the policy was about, with it bouncing around a lot as a result.
Barkley: I am curious – how would you decide between modeling a change in the target of the Fed’s actions (e.g. money supply vs ffr) as
a change in (or elaboration of) the structure of disturbances
vs
a change in the parameters of the model equations itself, e.g. a Markov switching model?
Good question. It strikes me it might show up as both. In the past, JDH was one of the main developers of the regime switching approach.
So, Jim, is it one, the other, or both?
Robert and Barkely, yes, there are lots of ways one can go. What the paper basically recommends is just calculate the R2 diagnostic on whatever model you were initially using. If it passes, great, if not, you need to modify the model in some direction, and which direction is sort of up to you.
On the specific question of fed funds volatility, it’s true that the 79-82 episode is the biggest single factor, and if you pick that up (e.g., with Markov switching) you’ll eliminate the biggest sins. But you find ARCH outside of that episode, as well as a declining trend in volatility.
Now, if I were really pushing my stuff, I’d call attention to SWARCH.
While ARCH and GARCH are useful for getting you a Nobel prize but really are only good for telling you the past, Stochastic volatility models are better at telling you the future. David Stoffer at the University of Pittsburgh has some pretty interesting item comparing GARCH to Stochastic volatility models.
Also, as a statistician I think that far too much is made about minor deviations from assumptions. Much of the time it doesn’t matter. Sure you can create nice counter examples, but in practice it really doesn’t make that big of a difference.
This line of reasoning is important enough for me to do background research. I need a few days, but it sure looks like it is right on track.
Well, I looked, and being an adaptive LMS filter designer, I caught on right away.
There is a metaphor we can use, the CAT scan. computer aided tomography. The CAT scan uses Jim’s method.
Start an xray beem through a person, and assume that density comes in chunks of 1/8 inch ply in the body. The recompute the data as if density comes in 1/2 inch layers of ply. You see a little drop in residual noise in your estimate. Then assume density comes in 3/4 inch density plys, and suddenly your residual noise jumps way up. This tells the algorithm that a 1/2 inch ply assumption is the minimum necessary to make the data appear like sufficiently like homoskedastic, separate distributions. It is the smallest chunk of bone your system can accurately measure.
When the algorithm comes up with the optimum 1/2 inch ply assumption, then is can reconstruct the best image of the bones.
Jim’s method leads to a kind of echo process in which economists can measure aggregate time series and reconstruct labor structure.
Econobrowser is hot on the trail, this is new stuff. Ultimately it leads to something called bond energy. It is the point at which our measuring tools (financial calculations) cannot be used unless we reorganize part of the economy.
Or, alternatively, it leads to the point at which economic exchanges cannot provide low variance estimates sufficient to use money technology; and the economy must reorg.