One of the most robust findings in international finance is that interest differentials do not point in the right direction for subsequent exchange rate changes. This means that dollar returns on say one year certificates of deposit in the US and in the UK are not on average equalized. In Chinn and Meredith (2004), we show that this anomaly — if it is one — disappears as one goes to longer horizons. This finding was discussed previously here.
In this post, I discuss new results regarding this finding, basing the discussion on Chinn and Quayyum (2012). The sample examined in Chinn and Meredith ends in 2000. Since then, the global financial crisis has introduced a tremendous amount of volatility and default risk into international financial markets. In addition, short and long term interest rates have descended toward previously unplumbed levels. (In addition, several of the exchange rates previously examined, such as the Deutsche mark, the French franc and the Italian lira, have merged into the euro). It therefore makes sense to re-examine the question of whether at long horizons, the previous results prove durable when a new decade’s worth of data is included.
Some Theory
It’s helpful to consider under what conditions expected dollar returns should be equalized for securities denominated in different currencies. This is essentially a no arbitrage profits condition, so it would require (1) no barriers to the free flow of financial capital, and (2) the securities be treated as otherwise equivalent in terms of default risk, and risk associated with how returns correlate with wealth or consumption (formally, the exchange risk premium is zero). Then:
i = Δse + i*
Where i is the interest rate, Δs is the exchange rate depreciation, superscript e denotes (market) expectations, and the superscript * denotes foreign variables. This is equivalent to:
Δse = (i-i*)
Note that the condition states that expected returns are equalized, and equivalently expected depreciation equals the interest differential. Now, one can’t test whether these conditions hold, because one doesn’t observe the market’s expectation of exchange rate depreciation. Typical practice is to assume the actual, realized, exchange rate equals on average the expected (i.e., the rational expectations hypothesis).
Δs = (i-i*) + u
Where u is a random error term; under the joint UIP and rational expectations hypothesis (known as the “unbiasedness hypothesis”), the error term is a true innovation, that is an error term with mean zero, and is unpredictable on the basis of all information available at the time expectations are made. If one runs a regression,
Δs = α + β(i-i*) + v
this relationship (with a coefficient on the interest differential of unity) might not show up in the data, either because of risk or because market participants make biased forecasts of subsequent exchange rate changes.What do the data look like? In short, there is a voluminous literature saying at horizons of a year that indicates the β estimate is typically negative.
Empirics
We confirm that short-horizon result, but find that, as in Chinn and Meredith, interest differentials at the longer horizons point in the right direction. However, even at long horizons, the effect is more muted than in the earlier study. This contrast is shown in Figure 1.
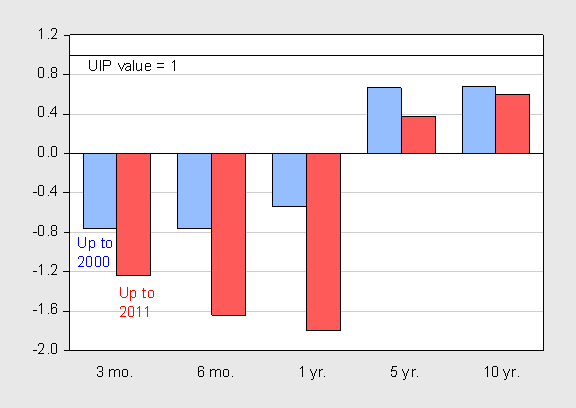
Figure 1: β estimates from panel regression of depreciation on interest differential, at 3, 6 and 12 month, 5 year and 10 year horizons, for sample extending to 2000 (blue bar), and 2011 (red bar). Panels do not contain same currencies in blue bars versus red bars. Source: Chinn and Meredith (2004), and Chinn and Quayyam (2012).
One can see why the results show up the way they do, by examining the correlations at the different horizons. I show the scatterplots at 1, 5 and 10 year horizons.
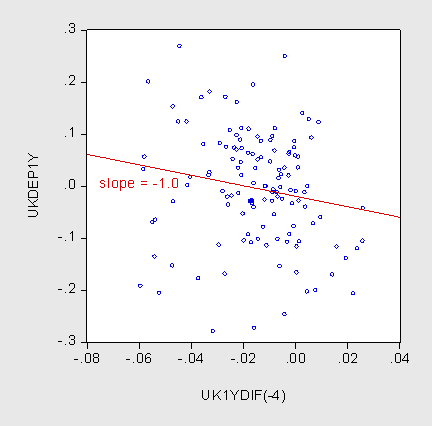
Figure 2: US-UK Ex post one year depreciation against one interest differential. Source: Chinn and Quayyum (2012).
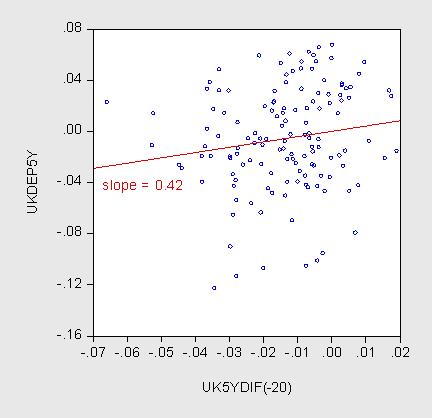
Figure 3: US-UK Ex post five year depreciation against five year constant maturity interest differential. Source: Chinn and Quayyum (2012).
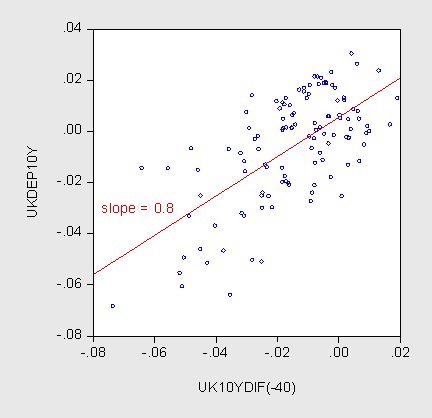
Figure 4: US-UK Ex post ten year depreciation against ten year constant maturity interest differential. Source: Chinn and Quayyum (2012).
Notice the progression; as the horizon gets longer, the slope becomes more positive. There are a number of reasons why this might occur. It could be that expectations are biased (this is examined in this paper). The other possibility is that the covariation between the exchange risk premium and the becomes less negative or more positive as the horizon is extended. This is the mechanism in Chinn and Meredith (2004), as the central bank responds to shocks to the within period exchange risk premium.
Why Do the Results Differ between Sample Periods?
Figure 1 indicates that the slope coefficient is lower in the more recent study than in Chinn and Meredith. There is a degree of noncomparability, as the currencies covered change from the early study (which includes the euro legacy currencies, e.g., French franc) to the late study. Nonetheless, it does seem that the coefficients at long horizon are lower when incorporating more recent data. However, rather than arising from the behavior of all the currencies, this phenomenon seems to be driven by the Swiss franc and in particular the Japanese yen. In Figure 5, I present the scatterplot for the five year horizon, for the Swiss franc.
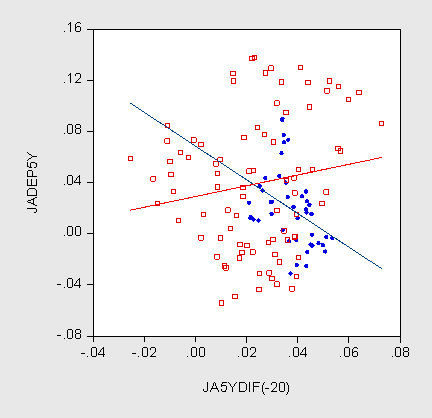
Figure 5: US-Swiss Ex post five year depreciation against five year constant maturity interest differential. Pre-1996 interest rates (red squares), post-1995 interest rates (blue circles). Source: Chinn and Quayyum (2012).
In other words, we might expect that the long horizon results that obtained in an earlier period of fairly high interest rates might be attenuated for other currencies as long term interest rates stay at historically low levels. After all, as of Monday, US, UK, Swiss and Japanese ten year benchmark yields at 1.65, 1.52, 0.55, and 0.81% (Source: FT, accessed 8/27).
Thanks Menzie, always interesting analysis. As a practitioner, albeit not currently in FX, another way to think about it is that short-term FX movements are often driven by the carry trade; and long-term FX movements bear out the fundamentals of inflation/price level. There’s a bit of bubble trading theory linking the two if those two hypotheses are right, and the skew surface usually supports this story as well.
AaronF: Yes, good point. The carry trade is essentially exploitation of the fact that unbiasedness does not hold; see discussion in this post.
In your regressions, do you allow for the possibility that the interest rate differential is endogenous? Some of the largest players in the FX market are also large players in international bonds markets. The disturbance term captures “insider knowledge” that participants have, such as expectations about what central banks will do in the future; and that may be correlated with the (i-i*) term. Would it make sense to use something like the difference in GDP growth rates as an instrument for (i-i*)?
Brian: In this set of regressions, we have not statistically take into account the endogeneity. That endogeneity is implied by the Chinn-Meredith model, for instance. However, typically, IV estimation has only reduced, but not eliminated, the deviation of point estimate from the posited value of unity (see e.g., Sarantis, JIMF 2006). Your suggestion of using GDP growth as IV can be rationalized in a Taylor rule model, for instance, and might do better than those used in the literature, although the advent of the ZIRP suggests these might prove to be poorer IV in recent times.
This is an interesting rationalization of Keynes theory of the intresec parity in exchange rates.The time lags before depreciation are unevenely spread and current accounts deficits do not seem to play a major role when the aassumptions include:
“no barriers to the free flow of financial capital”
What are the R2 of the different regressions?
Consider the following dynamic:
Central bank pushes local interest rates down, encouraging carry trade capital outflows.
Carry trade outflows cause the currency to depreciate. Initially, carry traders gain both interest differential plus currency gain, spurring further carry trade outflows.
Eventually, adjustments of asset allocations are completed. At that point, net capital outflows cease and the currency starts to move back to PPP, appreciating.
Currency appreciation reduces the desirability of foreign investment (by causing carry traders to suffer an exchange rate loss) and causes “backwash” of carry trade flows.
Currency futures rates are set by arbitrage flows during the whole time, providing profitable currency speculation opportunities.
Hi Menzie, just a quick pointer to an editing problem. You write: “(In addition, several of the exchange rates previously examined, such as the Deutsche mark, the French franc and the Italian lira)”… you meant to write that these currencies have since been merged into the common euro currency.
Regards!
Hello Menzie,
I would expect that the long-term unit value of Beta would be obtained but only subject to a stable (in % of GDPs, or zero in levels?) of the net international investment positions. However, these have been rising sharply in several major economies since the early 2000s, think of China and Japan.
Anonymous (8/28, 12:57PM): The R-squared are reported in the paper; for the short horizon are about zero, and range up to about 0.4 at the ten year horizon.
don: The point is that a no-arbitrage profits condition combined with rational expectations should yield a unit coefficient, in the absence of an exchange risk premium. The fact that the carry trade is profitable is consistent the failure of the no-arbitrage condition (as well as the beta coefficient less than unity).
Patrick_VB: Thanks for the editing tip; that’s fixed.
Regarding your hypothesis, that might be the case. Once one departs from the null of the unbiasedness hypothesis, one can speculate endlessly about why the coefficients vary. One needs a specific model to say why the beta coefficient varies.
Wholly unrelated to the post, but a question for Menzie:
How is the Paul Ryan lie about the Janesville plant playing in Wisconsin? Are the local papers and tv stations mentioning it?
(As background, Ryan has been claiming, and said in his RNC speech, that Obama promised the Janesville plant would stay open but it closed. Obama visited in early 2008. GM announced the plant would close in October 2008 and it closed in December, before Obama took office.)
“The point is that a no-arbitrage profits condition combined with rational expectations should yield a unit coefficient, in the absence of an exchange risk premium. The fact that the carry trade is profitable is consistent the failure of the no-arbitrage condition (as well as the beta coefficient less than unity).”
Agreed. I think your empirical results just confirm the presence of exchange rate risk. The arbitrage condition I was referring to is covered interest arbitrage, which locks the futures market exchange rates to the spot rates. Thus, the futures rates always meet the zero-profit condition. The fact that the actual future spot exchange rates don’t is evidence either that expectations are not rational or that the futures exchange rate is determined entirely by covered interest arbitrage and contains no information about expectations of future spot rates. I prefer the latter explanation. That is, when bets by no-risk arbitragers are pitted against those by naked exchange rate speculators, the former dominate to such an extent that the influence of the latter cannot even be discerned.
We may be saying the same thing in different languages.
Menzie,
I wonder if your long horizon result can be explained by the claim that purchasing power parity, if it holds at all, will tend to hold in the long run. There is certainly some evidence to that effect and if interest rate differentials reflected inflation differentials over the long term, then the exchange rate would tend to follow the interest rate differential.
don: I see. That makes sense, and is consistent with Tsiang’s “modern theory” (from the 1950’s I think), but inconsistent with asset based approach.
Rich Stryker: Well, it might be PPP is holding well now, but unbiasedness doesn’t seem hold. I think it’s a matter of when monetary shocks are large relative to other shocks that unbiasedness holds (clearly that requires long run PPP to hold).