Today, we are pleased to present a guest contribution written by N.R. Ramirez-Rondan and Marco E. Terrones (Universidad del Pacifico).

There is well-established literature that documents the failure of the uncovered interest rate parity (UIP) condition. While a host of factors have been identified as possible reasons behind this result, the role of uncertainty is not fully understood. This column reports evidence that uncertainty is a key omitted threshold variable whose inclusion results in the UIP condition holding during low-uncertainty periods but does not during high-uncertainty periods.

Over the past four decades, the validity of the UIP condition has been extensively examined, but with mostly unfavorable results. Empirically, the UIP condition has been tested by regressing the (expected) change in the bilateral exchange rate on the short-term deposit interest rate differential—the so-called Fama regression. While the slope coefficient implied by the UIP condition is equal to one, most empirical studies report that the estimated slope coefficient is either negative or smaller than one. This finding has been labeled the UIP puzzle.

Several factors have been identified as possible explanations for this puzzle:

1. Most empirical studies have examined the joint hypothesis of UIP and rational expectations. It is argued that only under this joint null hypothesis, the slope coefficient must be equal to one. There is, however, ample evidence that suggests the failure of the unbiasedness hypothesis—since prediction errors are often negatively related to the interest differential so that estimated slopes are negative.
2. Some studies have noted that the Fama equation may be omitting one or more important explanatory variables. Some researchers have shown that a time-varying risk premia term resulting from risk-aversion, non-standard preferences, or disaster risk needs to be included in the Fama equation. The exclusion of such a term in the Fama regression is likely to bias the slope coefficient downward.
3. Other studies have explored the presence of non-linearities in the Fama regression equation. The presence of non-linearities was justified as the result of transaction costs or limits on speculation.

In new research, we examine the relationship between macroeconomic uncertainty and the UIP condition using an extensive dataset for a sample of advanced and emerging market economies (see Ramirez-Rondan and Terrones, 2019). There is evidence that uncertainty influences key macroeconomic (aggregate saving and investment) and financial (financial and credit market conditions, and currency risk) variables. Thus, there is the possibility that uncertainty is an important omitted variable that could affect the Fama equation in non-linear ways. In particular, the econometric analysis postulates a panel threshold regression model and utilizes survey-based exchange rate expectations and news-based measures of macroeconomic uncertainty.

The Fama Threshold Regression Model

The UIP condition states that the returns in the local currency of an asset denominated in both local and foreign currency must be equal. Thus, the following ex-ante Fama regression equation should hold in a panel,

                                           ,

where the sub-index i and t+h refer to country i in period t+h; s-hat is the (log) survey-based exchange rate expectation;  i and  i* are the domestic and foreign interest rates for a fixed asset that matures in h periods;  is an unobserved country-specific fixed effect; and  is an error term. When the intercept α is equal to zero, and the slope β is equal to 1, then the UIP hypothesis holds in the data.

To examine the effects of uncertainty on the ex-ante Fama regression equation, we amend (1) to include macroeconomic uncertainty as a threshold variable that splits the sample into two regimes. Thus, the ex-ante Fama threshold regression model is

where q_it  stands for macroeconomic uncertainty in country i, γ is the threshold parameter which needs to be estimated along with the other parameters in the regression equation, and 1(.) is the indicator function, which takes on the value of 1 if the inequality inside the bracket is true, and 0 otherwise.

We collect data for a sample of fourteen economies during 2003:1-2018:12. The country composition of this sample is determined by the availability of the macroeconomic uncertainty data.

Baseline results.

Our baseline results suggest that:

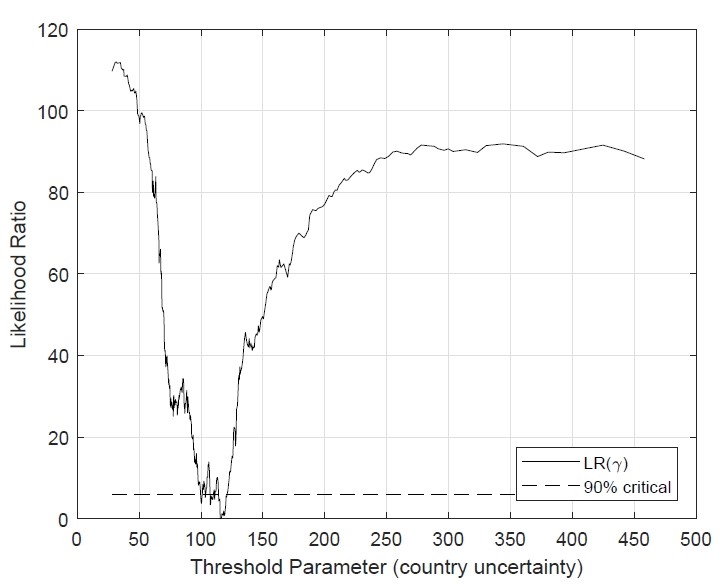
• There is a single uncertainty threshold which is highly significant. This uncertainty threshold splits the regression sample into two regimes which we denote the “low-uncertainty” and “high-uncertainty” regimes. The asymptotic confidence intervals for the threshold parameter are tight, which indicates high precision in the estimation (Figure 1). Moreover, there are no additional thresholds beyond the one we have reported.

Figure 1. Threshold estimate and its confidence interval

• The slope coefficients in the two uncertainty regimes are significantly different. The estimates of the slope coefficient in the low-uncertainty regime are positive and are not statistically different from one in most cases. In contrast, the estimates of the slope coefficient in the high-uncertainty regime are negative and statistically different from one.
• The panel threshold Fama regression model is preferred to the panel Fama regression. This is because the null hypothesis of a Fama linear model is rejected in favor of the threshold regression Fama model with two regimes, whereby the slope estimates in each regime are statistically different from each other. It is worth noting that the difference in constant estimates is significantly different from zero; as a non-zero constant is usually related to the presence of differentiated taxes, among other variables.

 

Are these findings robust?

We examine whether the inclusion in the threshold Fama regression model of other variables that might be related to the time-varying risk premium (such as capital controls, exchange rate flexibility, and terms of trade) affect the main findings above.

• Do capital controls matter? Capital controls have often been used by countries to mitigate the exchange rate effects of capital inflow surges or sudden stops. The inclusion of this variable in the threshold Fama regression equation suggests that capital controls tend to appreciate the domestic currency, leaving the baseline results largely unchanged.
• Does the selection of an exchange rate regime matter? There is a literature that suggests that countries with flexible exchange rate regimes should have more depreciated exchange rates than countries with fixed exchange rates. When we include a de facto exchange rate regime proxy in the threshold Fama regression equation, we find evidence of a positive and statistically significant association between the exchange rate regime and the expected change in the nominal exchange rate. The main baseline findings remain, however, unchanged.
• Does the evolution of commodity terms of trade matter? Favorable commodity terms of trade is another variable that has been associated with more appreciated exchange rates. To examine this possibility, we include the annual percentage change of commodity terms of trade for each country as an additional regressor in the threshold Fama equation. We find that there is a negative and statistically significant association between the change of commodity terms of trade and the expected change in the nominal exchange rate. Perhaps more importantly, the main baseline findings remain unchanged.

More research is, however, needed…

We find evidence that macroeconomic uncertainty is an important threshold variable that could help us understand the UIP puzzle. When using a threshold Fama regression model, we find that the UIP condition holds in low-uncertainty periods but does not in high-uncertainty ones. The subtle effect of macroeconomic uncertainty on UIP suggests that both the linearity of the Fama regression model and the omission of macroeconomic uncertainty from this model might be at the core of the negative empirical results widely reported in the literature. Our findings are robust to the inclusion of other control variables.

Why does UIP hold in low-uncertainty periods but not in high-uncertainty ones? The theoretical literature is virtually silent on this, and our findings suggest that this could be a fruitful area for research. There are, however, indications that macroeconomic uncertainty can affect financial market liquidity, the volume of assets traded, and excess returns in currency asset operations. These effects are likely associated with the time-varying risk premia, but little is known about the specific channels through which this happens.

 

---

This post written by N.R. Ramirez-Rondan and Marco E. Terrones.