At the economics meetings here in San Diego this weekend, I learned about some very interesting new research on one of the core questions in finance and macroeconomics that had long puzzled me.
We know that some assets on average offer you a higher return than others. For example, over time you’ll make more money investing in stocks compared to bonds. This clearly is a consequence of the fact that stocks are riskier than bonds, for which stocks compensate investors by offering a higher average return. We also know that this compensation for risk changes over time in dramatic ways that are related to business cycles and credit booms and busts.
But understanding exactly what’s behind this has proven elusive. One idea is that an asset’s risk compensation depends on the covariance between its return and aggregate consumption. Something that pays off big when times are good is not as attractive (and therefore must offer a higher average return) compared to an asset that pays big when you really need the money. Although this is a compelling formulation from the perspective of many standard macroeconomic models, it has proven very difficult to reconcile with the observed data.
Another popular approach, known as the capital asset pricing model, suggests that what matters is an asset’s comovement with the overall market. According to CAPM, an asset whose biggest payoffs come when the market is doing well would be less attractive than others unless it offers a higher average return. Again there are elegant theoretical motivations for why such a relation should hold, and abundant evidence that something more is going on in the data.
Researchers Tobias Adrian of the Federal Reserve Bank of New York, Erkko Etula of the Federal Reserve Bank of New York (now at Goldman Sachs), and Tyler Muir of Northwestern University have a very interesting paper that will soon be appearing in the Journal of Finance that offers another perspective on what ultimately drives the market price of risk. They argue that the key economic agents whose arbitrage ensures that risk is priced consistently across assets are broker-dealers. Rather than try to explain risk-compensation in terms of the marginal value of a dollar to a representative consumer or investor in the economy, the authors suggest that we should look at the marginal value of a dollar to broker-dealers as a group. The motivation for looking at broker-dealers is that they are market makers across various asset classes, trade actively, and constantly monitor the evolution of economic activity. Broker-dealers are perhaps the closest entity to act as rational, forward looking and continuously well informed economic agents. In contrast, rational inattention or behavioral biases on the part of households might partially explain the failure of consumption-based models or CAPM.
The leverage of broker-dealers varies substantially over time. When leverage is high, it is easy for them to use their assets to meet margin requirements. That means that an asset that pays off big in times of high leverage is less useful to broker-dealers (and so must offer a higher expected return in compensation) compared to an asset that does better in times of lower leverage.
The graph below plots the series for broker-dealer leverage that Adrian, Etula, and Muir suggest we look at. If we thought of assets minus liabilities as the net equity of broker-dealers, leverage could be defined as the ratio of assets to net equity. This is not particularly a business cycle indicator– leverage actually increased during the recessions of 1970 and 1982 and during the first half of the recessions of 2001 and 2007-2009. Instead, abrupt drops in leverage were observed to follow specific financial events noted by the authors, such as the stock market crash of October 1987, the peso crisis in December 1994, the failure of Long Term Capital Management in the fall of 1998, the terrorist attacks in September of 2001, and the failure of Lehman in September of 2008.
 |
The authors then demonstrate that two-quarter changes in this leverage measure are remarkably effective in explaining the prices of various financial assets. The scatter diagram below summarizes the average returns on a variety of different asset groups, with assets higher on the vertical axis providing higher average returns over the last half century. The horizontal axis gives the predicted average return for that asset group based on its comovement with shocks to broker-dealer leverage. For example, if you look at stocks that have been doing poorer than others recently (the Mom 1 or Mom 2 group), their performance over the next 3 months is probably going to depend on events that are unrelated to those that will drive changes in broker-dealer leverage over those same 3 months. For this reason, these stocks are far to the left of other assets on the graph and according to the authors’ model are predicted to have a lower expected return than other groups. The actual average return (position on the vertical axis) for Mom 1 or Mom 2 indeed turned out to be quite low over this sample period. Portfolios constructed from short-maturity Treasuries also have little comovement with leverage which gives them lower expected returns according to the model, and such assets are also observed historically to offer lower realized returns. On the other hand, the prices of stocks with low market capitalization but high book-to-market ratios (such as S1B5 and S2B5) turn out to move strongly with leverage. A portfolio constructed from such stocks appears on the far right of the scatter diagram, and the model successfully predicts the high average return observed for these stocks.
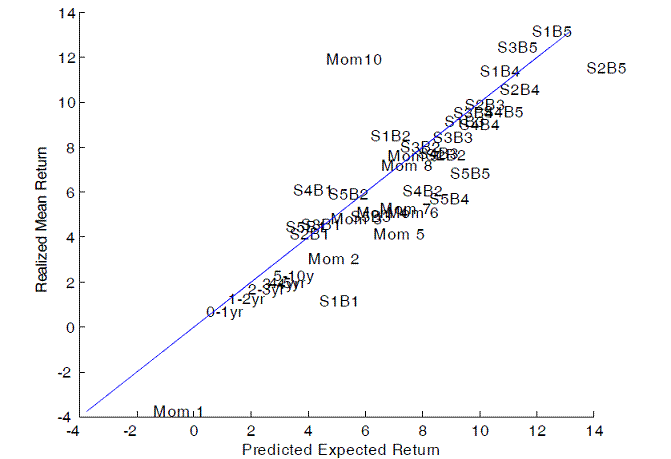 |
The authors find that the price of risk implied by this leverage factor is remarkably consistent across different portfolios with low cross-sectional pricing errors. The long-sought “stochastic discount factor” underlying modern finance theory may finally have been given a name and a face.
… which raises the question of why we allow government-backed TBTF banks to be leveraged speculators dominating the capital markets.
makes a lot of sense since broker dealer leverage is also a great proxy for market liquidity…
It is a very nice paper, but you go to far in saying that the stochastic discount factor has been given a name and face. What exactly is the economic interpetration? Is leverage a proxy for some underlying state variable? If so which one? Presumably leverage is itself endogenous and chosen by broker-dealers to maximize their return/wealth… As in any regression the question is, what is driving the variation in the RHS variable?
Errare humanum est, perseverare diabolicum
An interesting paper as it shows the asymmetry between the households investment behaviour and expected return and the brokers-dealers balance sheets. It does not show, how much leverage is tolerable for a single broker-dealer participant but gives an estimate of the aggregate exposure of the same as a global entity and its expected return.
It drives to the subject of liquidities as an independent variable, to exposure, to leverage. Subsequently it calls on the functions of BIS and a long series of Basle modules
Bloomberg « Basel 3 becomes Babel as conflicting rules undermine securities »
Of course conclusion and assumptions may sometimes be contradicted by empirical data and the Ferma French may not need to be cross checked up to 1930
Source: « Financial intermediaries and the cross section of assets return »
Bloomberg
« Almost All of Wall Street Got 2012 Market Calls Wrong »
Our good Pr Hamilton is right this paper gives a new face to “stochastic discount factor but few Econbrowser posts make it older:
Effects of Index-Fund Investing on Commodity Futures Prices.
Commodity index funds and oil prices
Commodity index funds and agricultural prices
Links for 2011-10-23
A modern model, may integrate dependant variables increment and independent variables increment, the paradox of St Petersburg , the theorem of impossibility and a test of Fourier mathematical sequences as it drives to the theory of chaos.
I am puzzled by your statement, “When leverage is high, it is easy for them (broker-dealers) to use their assets to meet margin requiremnts. ”
Leverage is being defined as assets/equity. So when leverage is high, a high percentage of the assets is being financed by liabilities. How is it that a high level of liabilities relative to assets makes it easy for them to meet margin requirements?
What’s on the balance sheet of a broker dealer? Oversimplifying a bit, Assets = Securities while Liabilities = debt. They are not like a bank with deposits on the liability side and loans on the asset side.
Regarding the S1B5 and S2B5 high book to market portfolios:
In good times assets rise relative to liabilities.
In bad times assets fall relative to liabilites.
A postive shock is associated with expected “expansion”.
A negative shock is associated with expected “contraction”.
High book to market stocks have relatively more defaulty risk. However, when the value of securities (assets) are rising relative to the value of debt (liabilities) then aggregate growth expectations are relatively high. Aggregate growth solves many problems for high default risk companies. It follows that the stocks of high default probability companies would be highest following a ‘leverage’ shock. This explanation is consistent with the returns in the chart and can be modified to explain the pattern for other types of securities.
It would be interesting to disaggregate the assets and liabilities of the broker dealers.
I’m not sure if this paper is getting the causation right. It is indeed the case that certain market shocks will cause both a decrease in financial institution leverage, as well as a outsized drop in some of the more exotic market factors.
But I don’t think it’s the sell-side institutions that are driving the pricing on the margin. Rather it’s probably the sensitivity of a certain class of sophisticated, but flighty (either for reasons of leverage and/or aggressive risk-management) buy-side institutions,
During certain market “risk-off” shocks, these institutions will withdraw much of the short-term funding they provide to broker-dealers (both in terms of selling off short-term paper as well as withdrawing prime brokerage accounts). At the same time many of them will de-leverage their positions (some of them even completely winding down if investors pull their capital).
Since these small class of sophisticated buy-side institutions make up a disproportionate number of both “exotic market factor” investors and short-term investment bank funders, you’ll see these two things move together.
A great example of this can be found in Andrew Lo’s paper about the quant crisis of 2007. Once again we found financial institution funding dry up (a lot in the form of structured credit vehicles) as well as a nosedive in many of the very esoteric quant factors.
Long story short, you’re looking at the wrong group if you think broker-dealers are mediating the pricing of secondary market factors. They’re merely downstream from the primary players.
“We know that some assets on average offer you a higher return than others. For example, over time you’ll make more money investing in stocks compared to bonds. This clearly is a consequence of the fact that stocks are riskier than bonds, for which stocks compensate investors by offering a higher average return.”
I’ve never really understood this. Why don’t the expected values equilibrate?
Stocks do not “compensate investors”; stocks are objects which are bought and sold. You’re saying that no one will buy them at a price which… what? Is so low that the EV (including risk) is less than that of bonds? So then the price gets bid up to the point where the EVs are identical. Right?
Gene: You can meet margin requirements by putting up any asset– doesn’t depend on your net worth, depends on whether you have some assets to pledge.
Ricardo: We’re talking here about a generalization of your theory. If people expect a lower value for future dividends, they’re not willing to pay as much for the stock. So a drop in the expected value of future dividends results in a drop in the current market value of the stock, just as you say. Likewise, if people expect a higher volatility of future dividends (might go up a lot but might drop a lot), they’re not willing to pay as much for the stock as they would for a stock with the same expected value of future dividends but less risk. So an increase in the perceived riskiness of a stock also results in a drop in the market value of the stock.
I wonder if it would be worthwhile to utilize this idea to construct a benchmark portfolio for mutual fund performance evaluation. Since a bulk of investment in mutual funds has transitioned from individuals to institutional investors and planned sponsors, it seems as if the representative consumer might not be the marginal price setter in the setting either.