With an application to accurately counting stimulus effects, for the benefit of the numerically challenged
Here I try to explain why dividing a number at a point in time by a cumulative number does not make sense (Warning: some understanding of calculus helpful). Reader Manfred defends the Weekly Standard’s calculation of dividing net jobs created at an instant in time by cumulative spending to obtain a dollars/job figure. Specifically:
What is a stock is the amount of jobs in an economy at a certain point in time. But the 3.5 million figure is the *change* in the stock; this is the amount that the stimulus fans said that would be created new during a certain period of time; thus, it is a flow, not a stock.
A similar calculation was undertaken by Professor Mulligan (rejoinder here).
So, in order to illustrate the oddities of such a calculation, let’s consider two variables, y-hat and x-hat, which are deviations of the variable y from baseline, and x from baseline respectively. I plot these two series below:
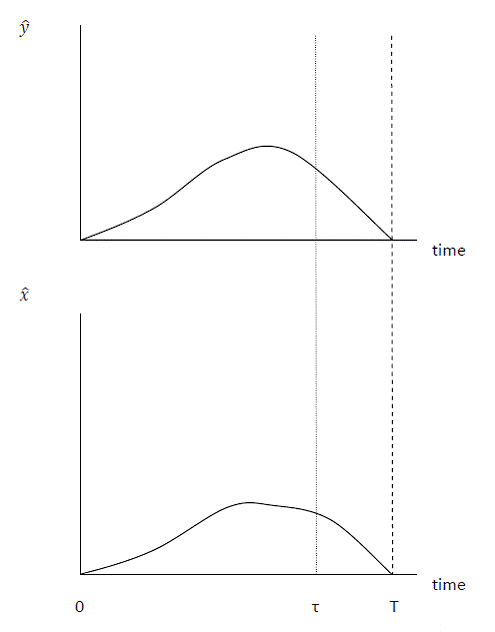
Now, Manfred would like to divide the cumulation of x-hat by y-hat. That is, divide the area under the curve x-hat up to a given instant, say τ, by the height of y-hat at τ. Technically, divide the integral of x-hat from 0 to τ by y-hat at τ. As my teacher used to say, nothing stops one from doing that. In this case, I’d just say common sense would stop you. Consider if one did the same calculation after time T. Then with a value of y-hat equal to zero, the number one obtains would be infinity.
I would say a more reasonable calculation is the integral of x-hat from 0 to τ divided by the integral of y-hat from 0 to τ. Formally:

Translate this into the issue at hand: Let y-hat be employment-years, and x-hat be dollars of spending per year. Divide the cumulative number of person-years of employment by the cumulative dollars spent to get dollars per year of employment. Then do Manfred’s and Weekly Standard’s preferred calculation, to obtain employment at time τ per cumulative dollars spent. Which object is of greater interest? I think the former
A short cut (that I learned in high school physics): Always keep track of the units the variables are measured in, to determine what it is that one is getting when dividing or multiplying.
See this post for the correct calculation of employment-years per dollar spent up to 2011Q1.
This is essentially same point made in the first chapter of Street-Fighting Mathematician – available to the innumerate as a free download. He notes a paragraph that compares the GDP of Nigeria to the stock market valuation of Exxon and takes it apart: GDP is a flow of value while net worth is a snapshot of asset value at a particular time, etc.
Something I learned a long time ago was that if you are trying to explain a relatively simple concept to someone and they are having trouble understanding it, it is probably due to poor teaching rather than a bad student. I think this principle aptly applies here.
Professor Chinn,
Thanks for the tutorial. If future tutorials fit with your idea of your site, I for one would appreciate it. Some of us may have enough calculus and statistics to follow basic economic arguments, although we may not have economics degrees, but we may not be able to follow graduate mathematics drills.
Jeff: Thanks for your opinion. I would be happy to compare my teaching awards to yours. My view here (as in my classes) is that I refuse to “dumb down” my exposition, and expect my students to have the math that was required to be an undergradate economics major.
Maybe an easy example to understand is the difference between a balance sheet and an income statement. A balance sheet is snapshot in time, while an income statement covers a period of time.
It is not a matter of “dumbing down” anything. It’s simply a matter of finding the clearest, most straightforward way to convey your idea. When you feel the need to introduce calculus into a problem that only requires basic arithmetic, I would say you are on the wrong path.
Jeff: If you say so. If you read the previous post’s thread, you will see I tried to explain these concepts in words, but certain readers were impervious, so I thought a couple graphs would be illuminating. Apparently, I was mistaken, in your case.
I think its simpler to use an example. If I say that my job has paid me $500,000. You’d probably wager that was a pretty good job! But if I said they made met that over the course of 10 years, and I actually only make $50k / yr it changes your opinion of how well-paying a job is.
Yes, technically its true that my company paid $500,000 for “one job” but to express like that and ignore time is misleading.
tried to explain these concepts in words, but certain readers were impervious.
This was exactly my point earlier. Your first thought is that there is something wrong with the reader, rather than something wrong with the words.
From the beginning you choose to confound the issue with an inappropriate analogy between “job-years” & “jobs” and stocks and flows. Then when reader Manfred was confused, rather then opt for clarity you give him this post, which, no, is not illuminating or clever or helpful, but just a bit of snobbery.
Prof Chinn,
I agree with your arguments. But in the light of this I always wonder if the heavily-followed debt/gdp measure makes sense? After all it compares a stock to a flow.
The entire point of the post is to ridicule rather than instruct. I’m totally ok with that. I don’t believe any of the readers here are too stupid to have understood the first explanation, and few are stupid enough to have required it. There are many too pigheaded and/or disingenuous to admit understanding it. That invites and deserves ridicule.
Jeff, don’t forget, Keynesians are experts on stock – flow issues: they invented IS LM. 😉
Mr. Jeff,
What is 5/0? What is 1,000/0? What is 1,000,000/0? Please re-read the Professor’s paragraph that includes this statemment,
“…Consider if one did the same calculation after time T. Then with a value of y-hat equal to zero, the number one obtains would be infinity….”
You don’t need calculus to explain that you have come to a logicaly absurd result. But the absurd result of infinity as an answer should push you to re-examine your approach to the calculation.
Jeff: Thank you for your comments. Clearly we have a pedagogical difference. The post includes a mathematical, a graphical, and a verbal, explanation. Gee … that’s what I do in my lectures. Well, I’m certain you can teach me how to teach better. I look forward to your tutorial.
I tutor kids in math. My experience is that many people can’t do it: they have trouble working with quantities, which is a basic issue I’m not sure can be addressed by anything. Other people grasp symbolic manipulation. That’s how most mathematicians work, with the classic divide between those who conceptualize problems and those who approach them through equations that stand for issues. It’s interesting to see how those struggles differ: one trying to put ideas in form and the other trying to understand what the form means.
Teaching math is hard. The materials generally suck. Most people try to translate ideas into words they can comprehend but the materials make that very difficult. I often find the best instruction is to say, “This is just notation. It isn’t very good. It really doesn’t mean much. You memorize it.” I try then to put the lessons always into much larger contexts. It’s weird, but I know people who design math curricula for kids and they focus on quantity issues – which I think are not resolvable for many people – rather than saying bluntly “Just remember this.” There is a reluctance to say that notation is somewhat of a game you learn to play with because materials always focus on conveying underlying meaning. Sometimes, just learning the form matters much more.
BTW, I find the best technique is to leap way, way ahead and talk about really difficult stuff. So the first time a kid is working with graphs and slopes and maybe factoring, I’ll talk about integration and how you can imagine an infinite stack of sheets of paper and the General Theory. I’ll talk about Hamiltonians and tracing the history of a particle. I’ll talk about mechanical advantage in sport: why a tall pitcher or a tall hitter has an advantage, why hockey players and soccer players can be smaller, why rowers are tall. I work with city kids so I talk about basketball and how sound travels and how you can see the difference between light and sound if you stand far enough away from the court where you can hear the ball bounce out of synch with the sound. Every bit in a math book relates to stuff that matters, not those stupid word problems. For those, you just need a strategy: write down in specific ways what they give you, etc., don’t think too much, etc.
I love to show fun stuff connected to the math. Like Gauss’ probably apocryphal schoolboy trick. What Archimedes realized in the tub. I show them how to multiply any 2 digit numbers in their heads quickly, which ties to what squares are, etc.
But adult innumerates? Fuhgettaboutit. Some of your commenters have less chance of understanding numbers than Snooki.
Ridicule and sarcasm can be a form of instruction, especially when the student knows, or should know better.
Casey Mulligan (who especially knows better), The Weekly Standard and Ted Nugent are engaging in these demonstrations of willful innumeracy because they are banking on some ideological readers not taking the time to understand why these calculations are so deceptive. Those who swallow it hook line and sinker without a moment’s metacognition need to be shocked into turning their BS detectors on. Sometimes ridicule and sarcasm is just the trick.
And if jonathan is right that adult innumerates will never understand these things, then they deserve double doses of ridicule and sarcasm for being so obstinate in voicing their ill formed opinions.
Incidentally, for those who may think even $116,000 a job-year is too high consider the following. Nominal GDP during 2011Q1 was $15,018.1 trillion at an annual rate. According to the broadest measure of employment, the household survey, there were 139.587 million people employed in the first quarter. That comes to about $107,600 of GDP per job-year in the first quarter. That’s because when you factor in all the costs of a job, ie. the benefits, profit, rent, interest, depreciation, etc. that’s what an average job really costs.
P.S. Chris, funny you should mention the debt to GDP ratio in this context. That’s an excellent point. Here’s what Robert Shiller said about that recently:
“That would clearly be nonsense. After all, debt (which is measured in currency units) and GDP (which is measured in currency units per unit of time) yields a ratio in units of pure time. There is nothing special about using a year as that unit. A year is the time that it takes for the earth to orbit the sun, which, except for seasonal industries like agriculture, has no particular economic significance.
We should remember this from high school science: always pay attention to units of measurement. Get the units wrong and you are totally befuddled.
If economists did not habitually annualize quarterly GDP data and multiply quarterly GDP by four, Greece’s debt-to-GDP ratio would be four times higher than it is now. And if they habitually decadalized GDP, multiplying the quarterly GDP numbers by 40 instead of four, Greece’s debt burden would be 15%. From the standpoint of Greece’s ability to pay, such units would be more relevant, since it doesn’t have to pay off its debts fully in one year (unless the crisis makes it impossible to refinance current debt).”
http://www.project-syndicate.org/commentary/shiller78/English
Units in pure time. Hmmm, now that’s meaningful (not).
You can continue to hide behind sarcasm if you like, but a quick search suggests your teaching techniques are not as flawless as you seem to think.
“A child of five would understand this. Send someone to fetch a child of five.”
— Groucho Marx
Jeff: Please feel free to explicate. I didn’t say I was a perfect instructor. Merely that I probably had more indicators of good teaching as compared to you.
@Mark A. Sadowski:
As for the debt to GDP ratio:
Yes, it is meaningful. It is an approximate measure for how long it would take to pay off the debt for a given GDP, if the interest rate was Zero. And the result doesn’t depend on whether one chooses quarterly, annualized or decadalized GDP for the ratio. Too bad that Shiller doesn’t mentioned this in his article. Instead he claims the results depends on the choice of the time period for the GDP. It only appears like this, since he himself uses the wrong unit. He uses % as unit for the debt to GDP ratio, which is the wrong unit. A time unit would be the right unit. For instance, for quarterly GDP the unit is $/(0.25 years), or for decadalized GDP $/(10 years) (if one uses years as time unit). If one uses the right unit for the GDP one gets the right unit for the debt to GDP ratio, and the debt to GDP ratio doesn’t depend on the choice of the time period anymore.
Note to myself: Always use the correct unit for the debt to GDP ratio.
Your reluctance to even consider that you have presented something unclear certainly implies you believe you have nothing to learn.
Jeff: Menzie is the master at making chicken salad out of chicken sh-t. It’s something the entire profession does well. Occams Razor is illegal in economics….
Menzie: how many undergraduate courses did you teach last year? One or two?
It’s easy to be a GREAT teacher when a) you hardly teach at all and b) you have a grad assistant to do most of the heavy lifting. Do you share all your teaching awards with the those assistants who do most of the heavy lifting?
Jeff: Hmmm, no response from Manfred so maybe the combination of calculus, graphical analysis, and verbal example has done the trick. I will say that in my experience, a reliance on “intuition” often leads to a mistaken belief of understanding, which is only dispelled when one examines the math.
Bobby: You can go to my website and find out how many undergrad classes I teach each year (2) as well as master’s (2). I’d like to see how much time it takes you write up the lecture notes, problem sets, midterm exams (2) and final exams.
By the way, I was a teaching assistant myself at one time; I think your assessment of heavy lifting is mistaken (not surprising as I suspect you are not a faculty member yourself).
Now, I am a Real Estate Broker, after 15 years as a Financial analyst and Manager with an MBA from USC, and an undergrad in Electronics from CAl Poly. I am not a teacher, but I have been a teaching assistant at USC. I “Get” math, but was shocked at the fellow MBA students who refused to grasp the basic and skeletal math offered there for Finance and Statistics. Unfortunately, it is a reflex reaction, often justified by peer pressure. I agree that simply calling it “Notation” and “Memorize this” works for the math averse. Then they don’t feel threatened by not understanding our universe in math notation. They just need to know enough to use the notation for the task at hand. I actually used this technique as a teaching assistant. I think a parallel is in the area of semantics. For instance, the word “Get” that I use above. From the context and usage, we obtain the operative definition, and that is all we need. We don’t need Websters, and the word origins, unless we are curious enough to want a precise definition, but that is not necessary for the use of the word. A similar word is “Hyper”. Don’t go to Websters for this definition, but the usage tells us it is “Overactive” and “Overwrought” and “Overexerting”, basically a noun for a state of “Over my tolerance”, looking for a consensus.
Finally, I do think that we need more “Teachertainment”. My best teachers kept me engaged by using multimedia and, yes getting me excited by extrapolating into wider applications to provide context. Context enhances learning. We all want to know why we are being presented with an idea, or notation, or fact or tool. We have been fighting this war since the 1960’s push for “Relevance”. So, when I taught, I added my own context to demonstrate the value of what I was teaching to the student’s future understanding of something. Integration? Yes, Integration is another way of saying Relevance. Point? Without context, a “Point” is infinitely small (mathematical definition of a point). Teaching, to me, is making the Academic into Real World. Thanks for the stimulating discussion.
another analogy
Suppose the stimulus is (just to make the math simple) 500 Bn
Suppose we create 10 million jobs;
simple division (5e11/1e7) yields $50K/job.
Suppose those jobs last 1 day.
Or
Suppose those jos last 3 years
I don’t think you need calculus (which is a lot less formidable then the concept of graphing deviations) to see that the 1st case is M Bachmann bridge in MN pork, and the second is FDR WPA.