Today, we are fortunate to have a guest contribution written by Laurent Ferrara (Banque de France and University Paris Ouest Nanterre La Défense) and Pierre Guérin (Bank of Canada). The views expressed here are those of the authors and do not necessarily represent those of the Banque de France or of the Bank of Canada.

---

Macroeconomic and financial uncertainty is often considered as one of the key drivers of the collapse in global economic activity in 2008-2009 as well as one of the factors hampering the ensuing economic recovery (see, e.g., Stock and Watson (2012)). While it has long been acknowledged that uncertainty has an adverse impact on economic activity (Bernanke (1983)), it is only recently that the interest in measuring uncertainty and its effects on economic activity has flourished (see, e.g., the literature review in Bloom (2014)).

A key issue relates to the measurement of uncertainty. A first solution is to measure uncertainty from news-based metrics. For example, this can be done by counting the number of newspaper articles that contain words pertaining to specific categories, for example, “economy”, “uncertainty” and “legislation”. This is the approach followed by Baker et al. (2013) to estimate daily uncertainty in the U.S. Another solution is to estimate uncertainty from the degree to which economic activity is predictable. This can be achieved by calculating the dispersion in survey forecasts or from the unpredictable component of a parametric model (see, e.g., Jurado et al. (2015) or Rossi and Sekhposyan (2015)). Moreover, uncertainty is also often proxied with a measure of financial market volatility such as the VIX (a measure of the implied volatility of the S&P500).

Despite a large number of uncertainty measures available in the literature, there is a fairly general consensus on the macroeconomic effects of uncertainty, in that uncertainty shocks are typically associated with a broad-based decline in economic activity. In particular, private investment is often estimated to exhibit a strong adverse reaction to uncertainty shocks. However, an interesting recent contribution can be found in the recent IMF’s World Economic Outlook chapter on investment that suggests that, since the onset of the Great Recession, the predominant factor holding back investment is the overall weakness in economic activity (the so-called accelerator effect) while financial constraints and policy uncertainty have a lower explanatory power (see also this previous Econbrowser post).

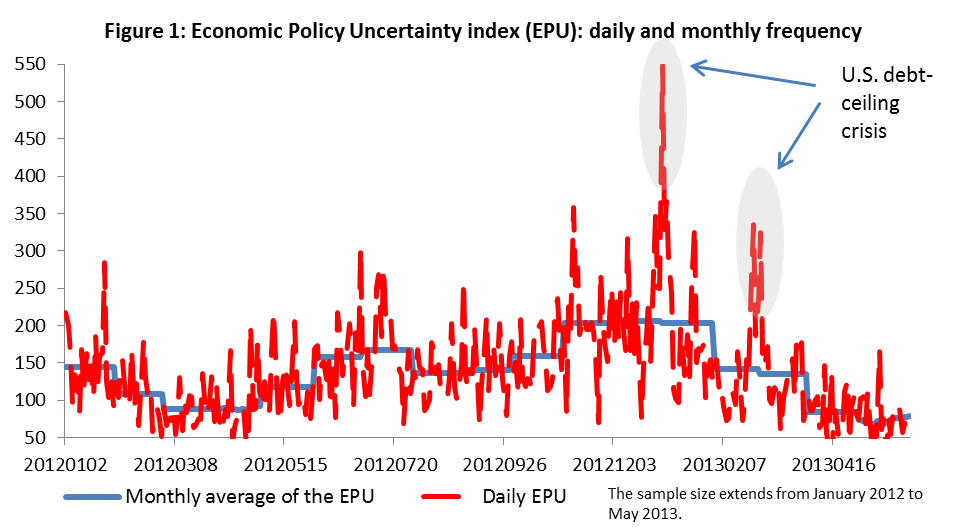
In a recent paper, we evaluate the effects of uncertainty shocks on the U.S. macroeconomic environment. In particular, we concentrate our analysis on the effects of high-frequency (i.e., daily or weekly) uncertainty shocks on low-frequency (i.e., monthly or quarterly) variables. In fact, it is natural to think that there could be insights to gain from the use of high-frequency data in that daily uncertainty measures are often characterized by temporary spikes that are not necessarily reflected in lower-frequency measures of uncertainty (see Figure 1). As a result, aggregating high-frequency uncertainty measures at a lower frequency could lead to a loss in information that may be detrimental for statistical inference. Likewise, if economic agents make their decisions at a high-frequency unit (say weekly frequency) but that the econometric model is estimated at a lower frequency (say monthly or quarterly), this could well lead to erroneous statistical analysis (see, e.g., Foroni and Marcellino (2014)). In the econometric jargon, this is dubbed as a temporal aggregation bias.

In our empirical analysis, we deal with the mismatch of data frequency between the U.S. monthly macroeconomic variables and the daily uncertainty measures we use (VIX and EPU) by estimating a mixed-data sampling (MIDAS) model that allows us to avoid aggregating the high-frequency data before estimating the models. A number of salient facts emerge from our empirical analysis:

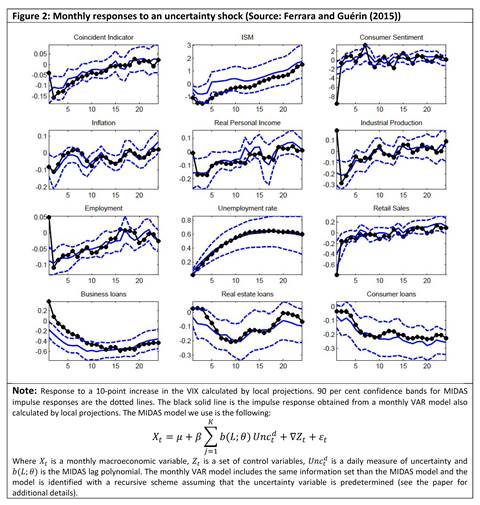
• The variables that respond the most to uncertainty shocks are labor market and credit variables (Figure 2). Other macroeconomic variables such as industrial production and survey data (e.g., ISM), also respond negatively to an uncertainty shock, but the responses are rather short-lived.
  
• There is no evidence for a substantial temporal aggregation bias in that responses from mixed-frequency data models typically line up well with those obtained from single-frequency data models. This suggests that there is no specific stigma attached to high-frequency uncertainty shocks.
  
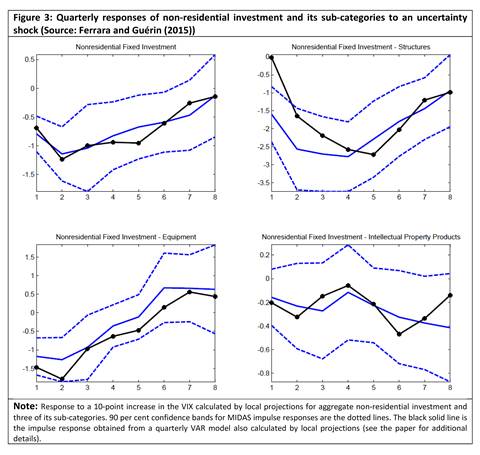
• As for the effects on quarterly investment, we look at various non-residential investment sub-categories. We find that the most irreversible investment category (investment in structures) reacts the most negatively to uncertainty shocks as opposed to investment in intellectual property products that do not react much in the wake of uncertainty shocks (Figure 3). This matches well with intuition, since in a highly uncertain environment, the most costly projects with the most distant return prospects are likely to be the first investment plans to be sidelined given that they cannot be easily undone.
  

Overall, a number of policy implications can be drawn from our analysis. First, to the extent that uncertainty shocks are not protracted, there is no disproportionate impact attached to high-frequency (daily) uncertainty shocks in that they yield similar responses than same-size low-frequency shocks. Hence, on average, one should not worry too much about the consequences of a temporary (i.e., daily or weekly) spike in volatility for the macroeconomic environment. Second, given that we find that investment in structures reacts the most to uncertainty shocks, this suggests that policy interventions designed to boost investment in the wake of uncertainty shocks should concentrate in priority on infrastructure investment.

---

This post written by Laurent Ferrara and Pierre Guérin.