Today, we’re pleased to present a guest contribution written by Yin-Wong Cheung and Wenhao Wang (City University of Hong Kong).
The Empirical Failure of UIP
Despite the fact that the uncovered interest rate parity (UIP) hypothesis plays a key role in model building and related analytical work in theoretical international economics, its empirical applicability has been seriously challenged. The Fama β-estimate (henceforth, the “β-estimate”) – the estimate of the cross-country interest rate differential coefficient – is commonly found to deviate from the value of one predicted under UIP, and is even negative in some instances.
Studies have noted that omitted variable bias can be a source of the empirical failure of UIP. Specifically, the canonical bivariate UIP regression should be augmented to, say,
where yt is the exchange rate change, ∇it is the corresponding cross-country interest differential, and zt includes control variables accounting for factors that affect the β-estimate. The representative control variables include empirical proxies for covered interest rate parity (CIP) deviations, risk premiums, and expectational errors. Not surprisingly, different empirical UIP studies employed different empirical proxies that were derived from similar or different theoretical models, and from either economic or non-economic data. To what extent these different empirical proxies capture the attributes of unobservable factors that are relevant to UIP?
Non-Uniform Effects
In a recent study (Cheung and Wang, 2020), we assess the empirical relevance of UIP with an empirical framework that allows for non-uniform effects due to model uncertainty and time-varying parameters. Technically, the Bayesian dynamic linear model (DLM) approach is used to accommodate time-varying parameters. And, a data-driven modified dynamic model averaging (DMA) procedure is used to assess the relevance of the empirical proxy variables and, hence, address model uncertainty.
We consider end-of-quarter observations of the exchange rates of the Australian dollar, Canadian dollar, Euro, Japanese yen, New Zealand dollar, Norwegian krone, Pound sterling, Swedish krona, Swiss franc against the US dollar, and the corresponding three-month forward exchange rates, and the three-month euro-currency deposit rates from 1990Q1 to 2018Q4.
From the existing studies, we collect a total of 27 empirical proxy variables; one proxy for CIP deviations, 15 different proxies for risk premiums, and 11 different proxies for expectational errors. Our empirical framework allows these proxy variables to display shifting levels of relevance and time-varying parameters. We focus on the behavior of the β-estimate in the presence of these proxy variables, and use it to infer the implications of these proxies for the empirical relevance of UIP.
Some Findings
Our empirical exercise indicates that the (augmented) UIP regression is subject to both time-varying parameters and model uncertainty – hence the set of relevant explanatory variables can change over time. We use the New Zealand dollar (NZD) case to illustrate some empirical findings.
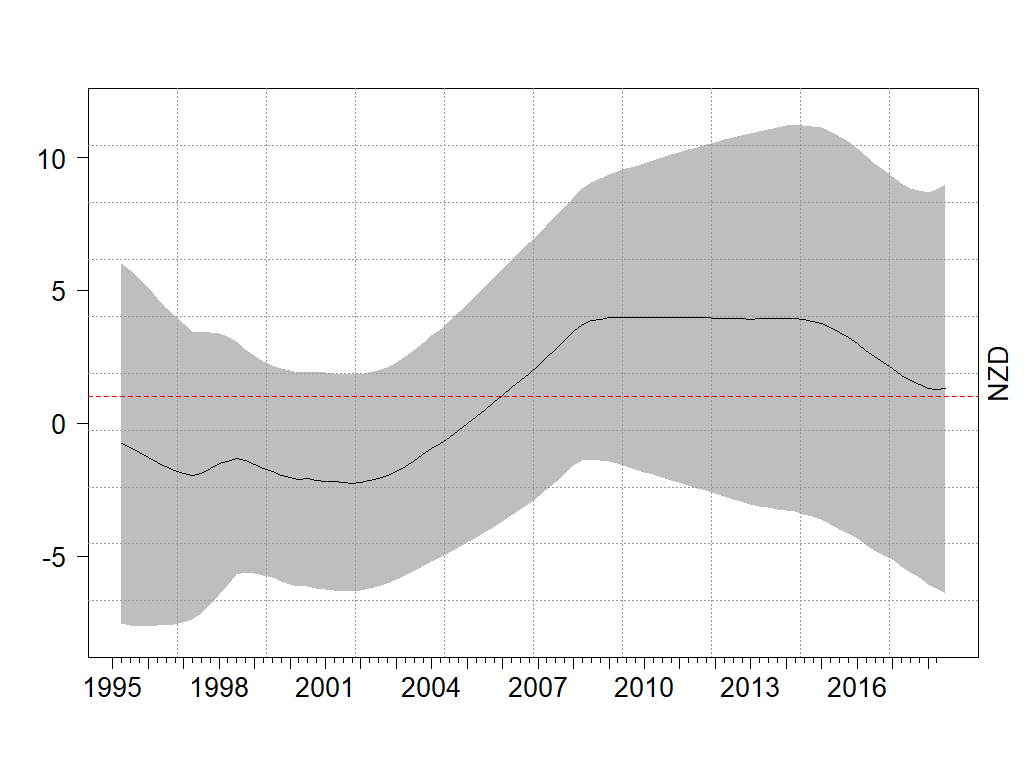
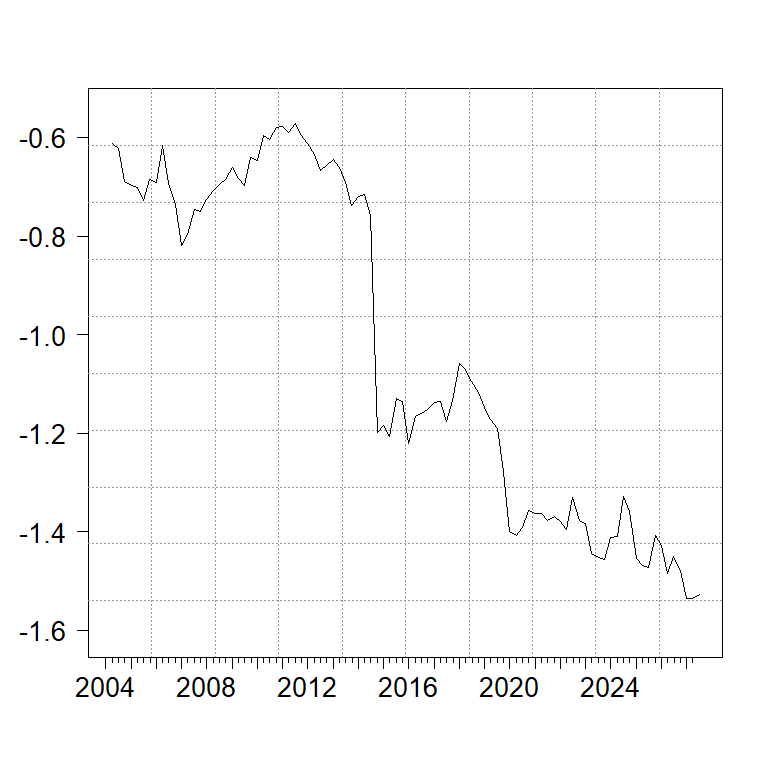
Figure 1. β-estimates from the Bivariate DLM UIP Specification – NZD
First, the UIP relationship, as indicated by the β-estimate, is time-varying. Figure 1 shows β-estimates (solid line; the dash horizon line is the 1-horizon line.) from the NZD bivariate DLM regression. The 95% credible region (gray area) is quite wide and makes it impossible to infer a precise value of β. Also, the β-estimate around the GFC turns to positive from negative (also, see Bussiere et al., 2018).
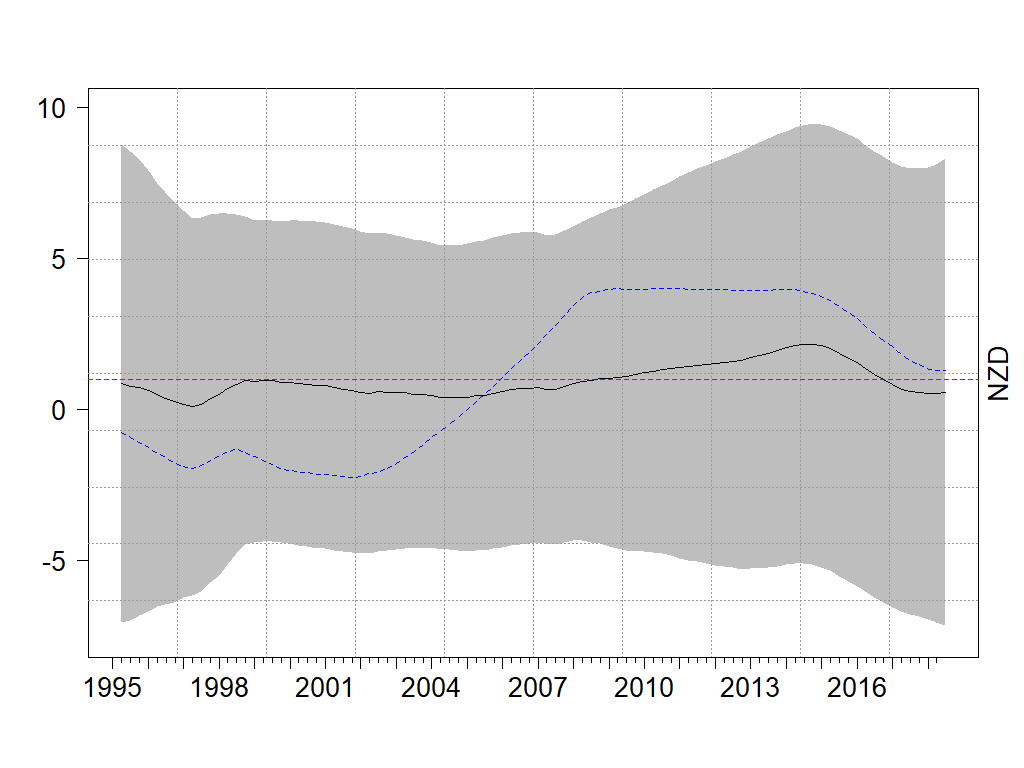
Figure 2. β-estimates from Bivariate and Synthetic Augmented UIP Regressions – NZD
Second, our results show that the inclusion of these proxies to the canonical bivariate UIP regression can yield a β-estimate closer to the value of one predicted under UIP. Figure 2 shows that, in the presence of selected proxy variables, β-estimates are closer to the horizontal line of one than those from the bivariate specification.
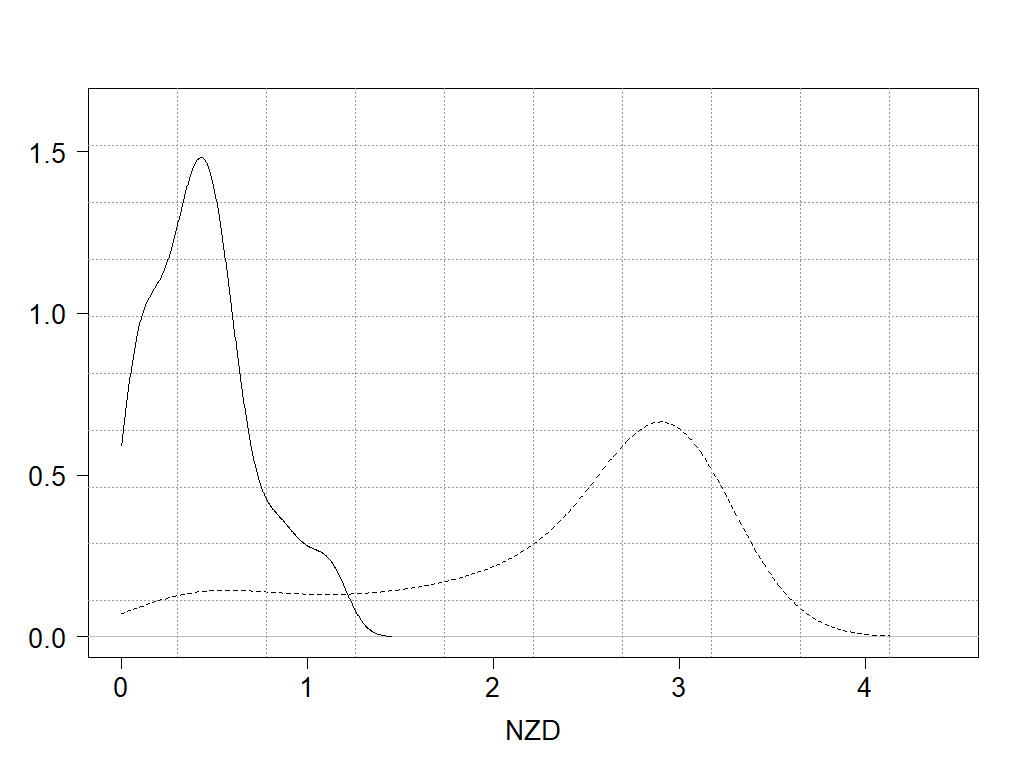
Figure 3. The Empirical Density Distributions of absolute differences from one – NZD
Figure 3 that plots the two empirical density functions of the absolute values of (β-estimate -1) of these two cases re-enforces the result. The presence of selected proxy variables moves the mass of absolute deviation from the theoretical value of one towards zero.
However, it should be pointed out that, while the presence of proxies reduces the deviation of the β-estimate from one, it does not reduce its sampling uncertainty.
Third, the set of proxy variables that alleviates the degree of UIP failure is not the same for all exchange rates under consideration. Further, both its composition, and the effects of its components can display wide variability over time.
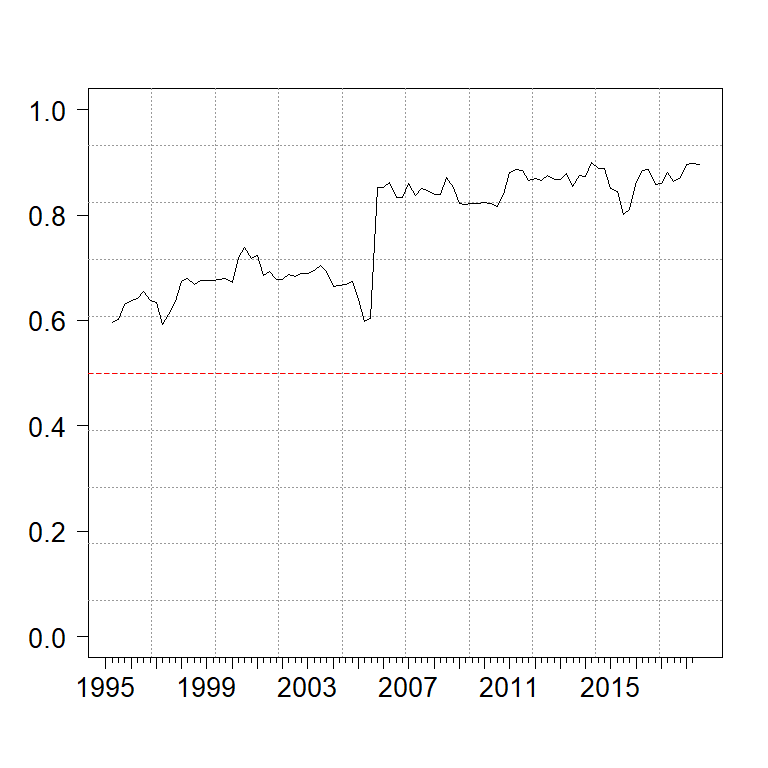
Figure 4. Retrospective Inclusion Probabilities of lagged cross-country growth rates – NZD
For the NZD case, Figure 4 shows the time-varying retrospective inclusion probability of including lagged cross-country growth rates – which is one of the macro risk proxies – in the model. The time variability of the degree of relevance, indicated by the inclusion probability, is quite apparent.
Figure 5. Model Averaging Retrospective Coefficient Estimates of lagged cross-country growth rates – NZD
The time variability of the coefficient estimate of this variable is depicted in Figure 5.
These findings corroborate the scapegoat theory that refers to shifting roles of determinants in foreign exchange markets, and is suggestive of factors that affect the arbitrage behavior underlying the UIP condition can change over time and exhibit time-varying effects. It is conceivable that shifting roles and time-varying effects of proxies for unobservable factors due to, say, changes in market perceptions can contribute to the difficulty of rectifying the empirical UIP failure. Further, the exchange-rate specific results present challenges to developing a general explanation for the observed failure.
Additional Discussion
Undeniably, our exercise is mainly an empirical one that highlights non-uniform effects. One relevant issue that we revealed but offered no insight into is the finding that the β-estimate tends to change from negative to positive after GFC. Why the switch in the coefficient estimate? Some comment on the reduced interest in carry trade activity. Bussiere et al. (2018) notes there is a change in the correlation between expectational errors and interest differentials. Our exercise affirms both time-varying effects and shifting roles of individual factors. However, we provide no substantive economic interpretation.
Extra efforts are warranted for assessing the extent to which these empirical proxy variables capture the attributes of the unobserved factors relevant to the UIP discussion, the conditions under which these proxy variables are good empirical proxies, and the factors that determine their shifting roles. Nonetheless, an empirical model for explaining UIP failure is likely to be one that allows for both a time-varying set of explanatory variables and time-varying parameters.
This post is written by Yin-Wong Cheung and Wenhao Wang.
Interesting study.
Something I am not able to discern from this post is how large the various risk premia are that are estimated. I get that their impact is time-varying as are the other factors, but how large are they? It is my memory from when I was reading this literature more closely and regularly than I do now that in the past the estimated risk premia that would make thinks work out for UIP were extremely large, far larger than independent estimates of actual risk premia. Is this still the case?
This is partly a follow-up to Barkley Rosser’s point. I can’t answer his question. But suppose you have two countries, A and B. Suppose we are looking at their exchange rates compared to a country C, which is an intermediate case. A is somnolent, with business activity low. A’s exchange rate vs. C is kept up by tariffs. B is active, with plenty of business activity. B’s exchange rate, which would otherwise be high relative to C, is kept down by trade openness. B’s monetary authority is also loose, to spur the economy, so the interest rate is the same as for A. Wouldn’t y_t for B be higher than for A, and aren’t the variables that are being included as controls missing this? In short, would a quantity control variable be relevant? Yes, expectations might be somehow configured to measure this, but it would be indirect.
Julian Silk: What’s true is that bilateral exchange rates being affected by only the respective two countries’ macrofundamentals is a special case.
Much more than any statistical test, UIP’s failure is demonstrated by my friends getting rich off the carry trade
Bob Flood: To be nitpicky, I’d say the failure of the “unbiasedness proposition” (rat-x + risk neutrality) is why our friends have gotten rich. Still a question whether it’s failure of rat-x, or a failure of risk neutrality (i.e., failure of UIP to hold).
Has this not been a problem all along? Without dragging in outside measures of things like risk perception, one is left unable to distinguish how much of what one sees empirically is due to a failure of ratex and how much is due to wildly varying risk premia, not to mention all the other stuff.
Barkley Rosser: The profession is divided – lots of finance (as opposed to international finance) people continue to work in the rat-x/unbiasedness framework.
Many private-sector exchange rate forecasts are based on UIP. FX forecasts are also notoriously terrible. That has always suggested missing variables, as the authors of the research reported here note. I glean from the comments on non-uniformity that forecasting models are likely to remain terrible. Clients demand forecasts, so forecasters will continue to offer them, showing off their good calls and hiding their bad ones, but reliance on such forecasts is likely to worsen investment performance by leading investor to think they have reduced FX risk when they have not.
I will admit to having worked in shops which provided such forecasts without any mention of the fact that they are, as a genre, are terrible. I was often told to pipe down when it came time for FX forecasts.
Good point, macroduck. I suspect that Menzie and Bob Flood and Jim Hamilton as well, all of whom have been in the biz of studying forex markts empirically at one time or another, would probably agreee that of all macroeconomic variables forex tates are probably the hardest to model and to forecast well. The whole enteprise hs long been shadowed by the study way back in 1985, I think, by Meese and Rogoff that showed that random walks generally do a better job of forecasting forex rates than almost any models, and they do not do so well either, although I know that Menzie has posted some more recent studies of models that have been able to beat random walks by at least a little bit, although none of them by all that much, if I am remembering correctly.