The Mankiw-DeLong inspired debate over the time series characteristics of GDP continues. [1] [2] [3] Here is a very long run (1867-2008) extension of my 1967-2008 quarterly analysis covered in this post.
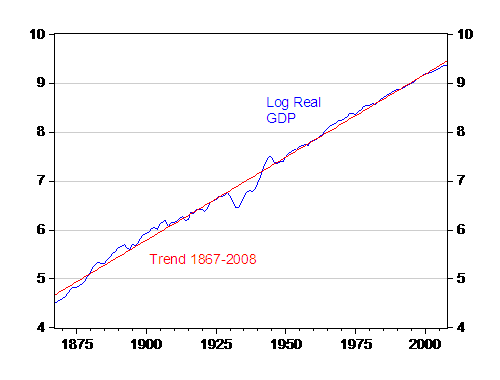
Figure 1: Log real U.S. GDP, 1867-2000, in billions 2000$. Source: GDP from Johnston and Williamson, and author’s calculations.
The Elliott-Rothenberg-Stock (1996) DF-GLS tests statistic (assuming constant and linear trend, lag length equal 1, selected using Schwartz Bayesian information criterion), is -3.3258. The 5%(1%) critical values are -2.988 and -3.5296. Hence, we reject the trend stationary unit root null at the 5% msl.
The Kwiatkowski-Phillips-Schmidt-Shin (KPSS, 1992) LM test statistic is 0.88306 (allowing for constant, trend, bandwidth=9, Newey-West using Bartlett kernel), where the asymptotic critical value is 0.119 for the 10% msl. Hence, we fail to reject the trend stationary null at conventional levels.
So, by the conventional statistical criteria, I would judge log real GDP as reasonably well characterized as a trend stationary process. This doesn’t mean that deviations couldn’t be long lived. The deviation from the trend depicted in Figure 1 is 0.912, which implies a half life 7.6 years. This is longer than the three years estimated using quarterly data over the 1967-2008 period. This result could be attributable to the fact that this long sample encompasses the Great Depression, as well as the Depression of 1893.
And of course, in all of this, I have not investigated asymmetries, nonlinearities, etc.
Technorati Tags: trend stationarity, difference stationarity,
unit root, GDP, and KPSS.
A small correction – the DFGLS has a null hypothesis of non-stationarity. I think you meant to say we reject the null of non-stationarity in favor of a trend stationary alternative.
RW: Yes, thanks for catching that. Fixed now.
I think the graph itself illustrates once again that the important matter is why the Depression was so much worse than before or since. If this recession is more similar to most recessions, then I suspect the three year estimate is reasonable. On the other hand, if this recession is more like the Great Depression, then 7.6 may even be optimistic.
I think that Paul Krugman rather muddied the waters by talking about unemployment. If you accept Okun’s Law, as he seems to, you hypothesize that the rate of unemployment depends on growth in GDP. Suppose log real GDP has a single unit root. Growth in real RGDP would be the first difference of LRGDP, and will not have a unit root – it will be trend stationary. Then by Okun’s Law, unemployment will also be trend stationary, possibly with a flat trend. Krugman might be thinking of the case where LRGDP has a unit root but no drift, but given that the series is trended you need to include some kind of trending term in each of your possible characterizations. The time series properties of unemployment don’t seem to tell you much at all about the time series properties of real GDP.
“If you accept Okun’s Law, as he seems to, you hypothesize that the rate of unemployment depends on growth in GDP.”
Then how do you account for the 2002-07 expansion, where GDP growth was very weak, but unemployment dipped well below 5% for a long time?
Dumb question (I’m an engineer, not an economist). In this sort of argument, wouldn’t it make more sense to analyze real GDP growth per capita instead? It seems to me that variability in population growth clouds the issue.
i liked the data minzie put up several months ago linking houshold wealth with consumption. while nost of this post is certainly beyond my level of knowledge it seems like we are likely to rebound more slowly due to the wealth destruction and boomers that need to replenish the nest egg over the next ten years
I keep making the same points on this debate;
1) The DeLong-Krugaman-Mankiw argument is not about trend-stationarity; the debate is about the bounce-back from the recession. (See Mankiw’s original post.)
2) The time-series properties of recessions are not like those of expansions. Beaudry and Koop have published on this. Durland and McCurdy have published on this. Dueker has published on this. Potter has published on this. We get similar conclusions if we look at Hamilton’s regime-switching models. All imply that recessions are much more transitory than expansions.
3) If you want to argue that the current recession will not be transitory, you do not find support from the kinds of recessions we have seen since WWII. There may be reasons to think that this recessions “is different.” But Mankiw’s claim that post-War data provides support for such a view makes no sense.
This GDP unit root debate seems wrong to me. What we are interested in is the rapidity and magnitude of response of GDP to a control variable, such as spending stimulus or quantitative easing (I guess interest rate policy is down for the time being). So, we need to consider the relationships between the target and policy variables in some system of equations. This includes both the long run statistical equilibrium (‘cointegrating’ relationships) and the associated short run error or equilibrium correction process.
What do the univariate time series properties of GNP tells us about those things. Nothing as far as I can tell. What am I missing?
The number of observations we have on GNP are too small to determine whether GNP really has a unit root or not. Unit root econometricians think it is close enough so that using unit root and one of the available cointegration approaches will be more efficient and robust than assuming any kind of stationarity. But that by itself does not change the modeling or estimation process much, if you have enough exogenous variables for an identified system.
Look at the book ‘Unit Roots and Cointegration’ by Hatanaka, or recent work by Katarin Juselius. Also chapter 9, section 9.6.1 of Johnston’s intro text, fourth edition.
If I am wrong, what am I missing?
Let’s get real, there has been severe damage to our economy and the banking sector in particular is severely damaged. Anyone who thinks we are going to have a robust bounce back is crazy. When you look at the initiatives this administration is proposing – higher taxes, cap & trade, etc – they all qualitatively should lead to lower growth in gdp and productivity. Add in a structural change in consumer behavior due to many people losing 40% of their net worth, it is very unlikely that growth in output or employment over the next 5 years will be as good as the historical average since the 80’s. On the other hand, it’s always possible there will be some technological advance that will boost productivity, barring that we are looking at a very stagnant economy. How’s that for hope and change?
Very interesting.
SvN is right that the surface debate (and the politically contentious one) is about the bounceback, and the unit root hypothesis is simply being used as one input to that debate.
But still, that’s the interesting part of it – because without a bit of theory to talk about, we are just making assertions about the future and then waiting to see if they come true.
I am surprised that Menzie’s long-run analysis shows such a clear trend stationary result, but he has demonstrated pretty solidly that this is what the data indicates.
My question then is: what are the underlying mechanisms here? I wrote about a few of them here but there seems to be no firm consensus on the causes. If trend stationarity is as good a hypothesis as the above graph indicates, that must give us some guidance as to which factors dominate in predicting growth rates.
My guess would be that background technological innovation (not sensitive to the amount of investment) and population growth are probably more significant than investment and training factors; but it’s possible to propose mechanisms where any of these factors can give a trend stationary result, so more detailed modelling and testing is needed to be sure.
In addition to factoring in population growth there are several other things that would be of interest if one is trying to project this trend line into the future (and ultimately use it as a basis for policy recommendations).
First, is the definition of GDP. I wonder if the type of economic activity makes a difference. For most of the period under consideration GDP was closely associated with manufacturing and agriculture, in other words real “stuff”. In the past two decades this has shifted to personal services, intellectual property and financial services. As we can see from the current meltdown, much of the economic basis of this activity is not based upon things of fixed utility (or value).
So, do we need a different measure than GDP to accommodate this change?
Second, is the relationship of GDP to the availability of raw materials. For the period under consideration most raw materials have gotten cheaper as technological progress has made extraction and production more efficient. One can expect economic growth to increase when one of the most important inputs keeps getting cheaper.
There are strong indications that this era is drawing to a close. What happens when raw materials start to consistently increase in cost and become scarce?
Finally, for the period under consideration the US was mostly “empty”. Much growth was accompanied by expansion into the wilderness which allowed easy accommodation of rising population and access to untapped resources, especially land, timber, iron and coal. The US is now “full”. Population is expanding into sub-optimal regions, like the Southwest which are short of water and require lots of energy for air conditioning and transport.
Parts of the original industrial base of the US are now being abandoned, see Detroit, Cleveland and the rest of the rust belt. Similarly the corn belt is being emptied of farmers. We have never had a period before where populated areas were declining while the overall population was increasing.
So, is the chart a useful tool for future planning, or a historical curiosity?
J writes
“This GDP unit root debate seems wrong to me. What we are interested in is the rapidity and magnitude of response of GDP to a control variable, such as spending stimulus or quantitative easing (I guess interest rate policy is down for the time being). So, we need to consider the relationships between the target and policy variables in some system of equations. …
If I am wrong, what am I missing?”
The short answer is “a cointegrating relationship.”
Those that want to focus on the long-run (as opposed to recession bounce-backs, like Leigh Caldwell, above) care about the long-run determinants of growth. However, economic models do a lousy job of explaining (much less predicting) variations in average growth rates across decades or across nations. Much of the variability we see in the data is not well explained by variables that we can measure well. As a result, those well-specified “response to control variable” problems you’re thinking of get bogged down in omitted variable problems (among others.)
SvN said:
” economic models do a lousy job of explaining (much less predicting) variations in average growth rates across decades or across nations. Much of the variability we see in the data is not well explained by variables that we can measure well.”
I agree, but isn’t this debate about the likelihood of a short-run large magnitude change in GDP for this recession in this particular country? I do not see how the mere presence of an autoregressive unit root in the GDP series tells us much about that. Given the likelihood of structural change over a long time series, I am not confident that the debate about whether there is ‘really’ a unit root will ever be settled. I think the unit root hypothesis should be considered as an issue of what approximation is most appropriate for statistical analysis and modeling.
is the data quarterly? If so shouldn’t the half-life be 7.6 quarters i.e. 1.9 years?
Response to J:
“…isn’t this debate about the likelihood of a short-run large magnitude change in GDP for this recession in this particular country?”
Yes, I agree that this is what (some people, including myself) think the debate is about. But I didn’t think that was what your question was about. My apologies if I misinterpreted you.
Menzie:
“This doesn’t mean that deviations couldn’t be long lived.”
Agreed.
Thanks for following up with more hard numbers that we can replicate, for those of us scoring at home. Seems you like to use Eviews. I used that software while I was at wisconsin and found it great for time series. Unfortunately, I am stuck with S-Plus here at work. My favorite is matlab.
Andrea: The data are annual.
For those interested in another application of the ADF and KPSS, take a look at JDH’s paper on oil price volatility, “Understanding Crude Oil Prices”.
Anyone can tell looking at Menzie’s graph that output is trend stationary. I may not be able to define it, prove it, but we all know what it is when we are looking at it!
Anyone who has played around with unit models and generated graphs knows how odd looking unit root simulations look – they are ugly, twisting, crazy things. It would be very hard to capture Menzie’s graph with a unit root of some magnitude.
However, I am not too sure I care. Old Keynesians (with beards) never trusted the Hicks-Hansen long run/short run model anyway. We live in a world of liquidity traps, multiple equilibria, fixed prices, multiple disequilibria, trading at false prices, falling profit opportunities over time, excess saving caused by inequality and class warfare, and other obscure, dusty things that can make demand permanent as well as transitory.
can you please help me to answer these questions, i really dont know these questions.our prof gave us assignments,but since the first day of our school he’s never taught us. here’s what im worrying about, when we will not answer these questions, he’ll give us 5.0, huhu.
Are the following statements true or false? Answer: True, because,.. or Wrong, because…
a) If you have data generated from a non-stationary process, you can rely on the ergodic theorem and estimate moments by sample means.
b) If asset prices follow a random walk without drift, future asset returns are unpredictable.
c) A white noise process is an ergodic process.
d) A random walk without drift has constant unconditional expectation over time and is therefore a stationary process.
e) Grangers representation theorem implies that when modelling multivariate non-stationary time series, the equilibrium correction representation is the correct econometric formulation to be used for parameter estimation.
f) A structural VAR is always estimated in its primitive form. The primitive form is also used to compute impulse response functions.
g) For computing impulse-response functions in a structural VAR you only have to estimate the VAR in standard form and trace a one unit shock to the composite errors by iterating forward on the VAR equations.
i) Empirical evidence suggests that asset returns are serially dependent whilst squared asset returns are not.
j) Empirical evidence suggests that predictability of asset returns is possible especially in the short run.
k) If the Dickey-Fuller test rejects the null hypothesis of non-stationarity of the your original data series at the given significance level for all series, an appropriate modelling strategy would be to estimate a structural VAR in first differences.
l) Having not been able to reject the null hypothesis of non-stationarity in the first step of the Engle-Granger methodology you can conclude that the data series are cointegrated and estimate an equilibrium correction model.
Interpret the following test results
a) Computing the Ljung Box Q statistic using the first 10 autocorrelations of a series of asset returns yielded a test statistic equal to =12.43. Your conclusion?
b) Computing the Ljung Box Q statistic using the first 10 autocorrelations of a series of squared asset returns yielded a test statistic equal to =89.43. Your conclusion?
c) A researcher used the Dickey-Fuller test to test for non-stationarity of a time series of length T=100. The estimated model included no constant or time trend. The test statistic is equal to 0.90. Your conclusion?
d) The researcher in c) also included a constant and a time trend in the estimated model. Now the test statistic is equal to 0.2. Your conclusion?
e) A researcher wants to test a series of asset prices for random walk of type 3. He computes the variance ratio test statistic (Cambell/Lo/MacKinlay, p. 55, Formula 2.4.44) and obtains a value of the statistic equal to -0.05. Your conclusion?
e) The researcher computed the test statistic for another series of asset prices and obtains a value of the statistic equal to 3.34. Your conclusion?