Justin Fox has a excellent discussion on the problems in conveying trends in real activity in relative terms when the real magnitudes are expressed in chain weighted terms.
Chain indexing updates the prices used to calculate real output every year, rendering the choice of base year much less important and allowing for meaningful real GDP comparisons over periods of many decades.
This had a side effect, too, though. For reasons that I’m not going to get into here but that you can read all about in Whelan’s 2000 paper, “A Guide to the Use of Chain Aggregated NIPA Data,” the different components of real GDP can no longer be added together. That is, they can be added together but, except in the base year, they don’t add up to real GDP. As time goes by, the sum of the different parts of real GDP gets bigger and bigger relative to the real GDP total. So calculating manufacturing’s share of real GDP over periods of decades generates percentages that are effectively nonsense.
This issue is of varying degrees of importance, depending on how much relative prices change. If they don’t change much, then adding and subtracting and taking ratios of chain weighted indices do not yield very misleading conclusions. However, as I pointed out in several posts, when relative prices do change a lot, such manipulations can lead to very misleading conclusions; see [e.g. Political Calculations 1] [e.g. Political Calculations 2] [e.g. Political Calculations 3] [e.g. Political Calculations 4] .
Figure 1 compares the nominal manufacturing share (an acceptable calculation dividing dollars by dollars) to the real manufacturing share (a potentially misleading calculation dividing units of manufacturing value added by units of GDP value added).
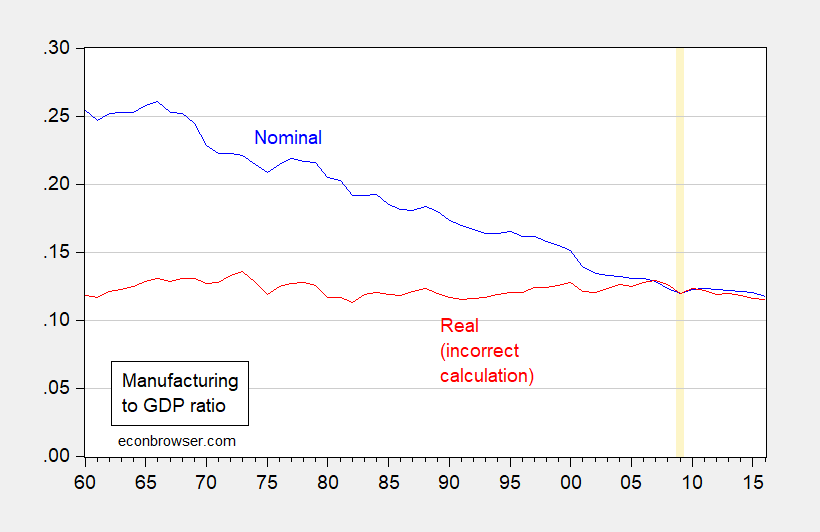
Figure 1: Nominal value added in manufacturing divided by nominal value added in GDP (blue), and real manufacturing value added in Ch.2009mfg$ divided by real GDP value added in Ch.2009GDP$ (red). Orange line at 2009. Source: BEA, author’s calculations.
Given the rapid decline in manufacturing prices — driven in no small part in the 1970’s through 1990’s by the rapid pace of computing power in information technology — the nominal share falls while the real does not markedly.
As Fox notes, the real ratio is not a correct calculation because the sum of chain weighted real magnitudes does not equal the chain weighted real aggregate, unless relative prices remain unchanged. What is a legitimate calculation is to take log of the ratio, which when expressed relative to a base year value, is a ratio of a cumulative percentage changes. This series, compared to the incorrect calculation, is shown in dark blue in Figure 2.

Figure 2: Real manufacturing value added in Ch.2009mfg$ divided by real GDP value added in Ch.2009GDP$ (red) and log real manufacturing minus log real GDP (dark blue), both normalized to 1960=0. Source: BEA, author’s calculations.
When the log ratio falls below the starting value, then the real manufacturing growth has cumulatively fallen short of cumulative GDP growth, so that manufacturing in this sense is less important than it was initially, starting most recently in 2014.
For those who want another way of depicting whether manufacturing has grown in proportion to overall GDP, one can check on the cumulative contributions to growth, and whether the cumulative proportion moves in line with the ratio at the starting point. This calculation is shown in Figure 3.
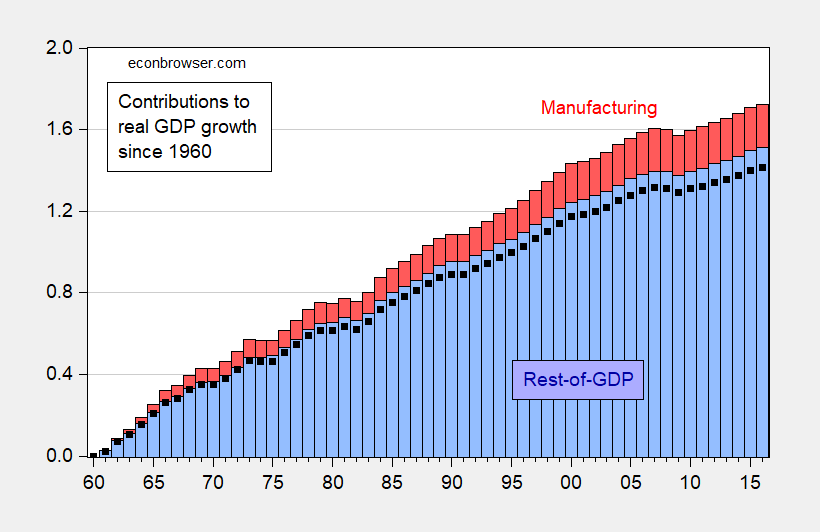
Figure 3: Cumulative contribution to GDP from manufacturing (blue red bar) and from rest-of-GDP (red blue bar) since 1960, and implied share for rest-of-GDP if manufacturing growth was in proportion to that in 1960 (black squares). Source: BEA, author’s calculations.
The fact the black squares are lower than the heighth of the blue bars indicates that manufacturing has declined as a share of economic activity. This approach constitutes an approximation, because the calculation of manufacturing contributions to growth involves dividing the change in real manufacturing output by lagged output (exactly analogous to Table 4 in this release).
So, there are a variety of ways to show how real sectoral activity has declined relative to overall real activity (I prefer log ratios) — but Justin is overall right: Friends don’t let friends calculate shares of real GDP.
Note this specific problem of real components not adding up to a real total occurs with chain weighted indices. If fixed weight real measures are being analyzed, then the adding up/dividing issue does not typically arise.
@ Menzie
Another one of your intellectually formidable posts. Unfortunately, between now and Thursday noon I will be “tweaking” my Econbrowser group NCAA bracket.
Menzie, I assume you will also be participating in the NCAA bracket?? I don’t see the name “Menzie” anywhere up on the group listings. If you need help, I found a “secret” (not really) website that would be helpful. If you promise not to tell Professor Hamilton or anyone else participating in this competition, I will email my “secret weapon” to you at least before Wednesday 18:00 to help you make or adjust your bracket. No, it is not Yahoo and no it is not ESPN. I will help you “fine tune” when you are looking for upsets. Gentleman’s agreement you will “keep it under your hat” and let me know in this comment thread if you want the info and I’ll shoot you an email as soon as I see the comment.
Moses Herzog: I’m afraid this is outside my area of expertise. A man has got to know his limitations.
@ Menzie
Hahaha, it’s so funny you said that. Yesterday I heard Warren Buffett promoting his NCAA tournament bracket prize, and Buffett said he was competitive, and one of his secrets to winning was “I never play Bobby Fischer at chess”. Still wish you were playing, just for the fun of it. Any man good at playing with numbers (as you are) would be good at this type thing.
https://en.wikipedia.org/wiki/Frank_Rosenthal
My guess is you lack interest in sports. My Dad was the same way.
well said Harry!!
“What is not reflected in this chart is changing relative prices. Because the prices of manufactured goods have gone up more slowly than those of other goods and services (think health care), Baily and Bosworth reasoned that manufacturing’s shrinking share of nominal GDP understates its continuing impact on the economy. They have a point, but their solution of relying on share-of-real-GDP numbers delivers some very strange results.”
A lot of times we teaches nominal v. real by assuming neutral inflation – that is the assumption that there are no changes in relative prices. Of course in the real world – relative prices change quite dramatically. Thanks for reminding us that this impacts how we should compare series across time.
Menzie,
Very nice post! I think innumeracy and statistical ignorance is the larger problem and one that is extremely common – such issues occur even amongst those with advanced experience and/or training as shown here and before (I seem to recall you once made a mistake where magnitudes compounded due to rounding in real values).
This could have been another great instance of you providing your work so readers can play with the data themselves in an attempt to assist them in even better understanding your message. It’s well known that facilitating hands-on opportunities often prove to be an effective instructional approach. It’s rather disappointing that you do not seem to be interested in sharing your work on this blog.
@ rtd
Menzie provides enough links, footnotes, and white papers, along with his own explanation, that those who genuinely (unlike you “rtd”) wish to pursue the math and the concepts involved can do so. All of this Menzie provides FREE to anyone with internet access, on top of his regular duties as a University prof.
Menzie provides everything on this blog FREE to jerks like you, but at a cost to Menzie of time and effort, all so sadistic nutjobs in dire need of attention can post comments like yours above. I for one am grateful Menzie does it, but for the love of God, have no idea why he does it when people like you have nothing better to do than needle a man who uses his time constructively to educate others.
https://www.youtube.com/watch?v=ks072waMayk
Maybe rtd, you should go look for “Stormfront” on the dark web, where I’m sure they’re very sympathetic to individuals who defend US Citizenship and Immigration Services writing racist policies. I think your internet “contributions” would be so much appreciated there.
Moses Herzog: Okay! But I don’t know why you’re so upset about me requesting Menzie to live up to his stated desire of wanting to do better with accuracy as it’s been a problem on here. My recent trouble in replicating coefficients from a very simple OLS model concerned me. This also made me realize the easiest way to verify I was properly duplicating Menzie’s constructed dummy variables was to ask Menzie to provide his work. This also helps Menzie I’m reaching his stated goal.
Your post/rant seems extreme and I am fine with whatever in the world it is you just attempted to convey aside from your comment regarding “individuals who defend US Citizenship and Immigration Services writing racist policies” if that line was to imply that i am such an individual. If your intent was not that I am such an individual, I do apologize for assuming such from your comment. However, if it is your intent that I am such an individual, I ask that if you have a question you would like to ask me directly and comment on my reply, please do so. But your approach is not a good look and I would appreciate it if you would refrain from assuming/misrepresenting/lying about my views. Again, if you have a direct question regarding these posts and/or my comments, I’ll likely answer. Thanks!
“But I don’t know why you’re so upset about me requesting Menzie to live up to his stated desire of wanting to do better with accuracy as it’s been a problem on here. My recent trouble in replicating coefficients from a very simple OLS model concerned me.”
Did you get the issue here? It is certainly not about regression coefficients. And expecting “accuracy” with respect to relative shares when relative prices have changed over time strikes me as completely missing the point here.
The coefficients reference requests for data on a prior post.
Accuracy is referencing Menzie consistently having errors in elementary data manipulation and/or blogging in general. As I stated, Menzie had issues with real vs. nominal values in a post quite some time ago.
Menzie I’m confused by your note for Figure 3. It says: Cumulative contribution to GDP from manufacturing (blue bar) and from rest-of-GDP (red bar)…
But the labels on Figure 3 show manufacturing in red and rest-of-GDP in blue.
2slugbaits: Good point, my mistake will correct.
Isnt the calculation of the relative share of manufacturing in GDP affected by the explosive growth of the financial sector itself?
If we rerun the number excluding the financial sector, a sector that has greatly expanded in terms of flows through it, with its own ‘productivity’ statistics and pricing changes too, you would see a different graph. Worth looking at manufacturing and other matters in this way it seems to me.