Today we are pleased to present a guest contribution written by Carlos Vegh (Chief Economist), Guillermo Vuletin, Daniel Riera-Crichton (economists), Juan Pablo Medina (consultant), Diego Friedheim, Luis Morano, and Lucila Venturi, in the World Bank’s Latin America and the Caribbean unit. The views expressed herein are those of the author and should not be attributed to the World Bank, its Executive Board, or its management.
In light of recent political and institutional uncertainty worldwide, lower commodity prices, growing cost of foreign debt, slowing external demand from major trading partners, and an increase in the frequency and intensity of natural disasters due to climate change, the perception of risk in emerging markets is as high as ever and calls for comprehensive risk management strategies. Given the very heterogeneous risks faced by emerging markets, finding a unifying and policy-relevant framework as a key first step to any efficient risk management strategy becomes a quite challenging task.
In a recent report (Vegh et al., 2018), the World Bank offers a useful framework for risk management based on the degree of uncertainty behind the different shocks confronted by emerging markets. As summarized in Figure 1, the report distinguishes between risks that are predictable (i.e., those that have a known distribution or “known unknowns”) from those that are completely unpredictable (i.e., when there is no prior about the shape or even the existence of an underlying distribution or “unknown unknowns”). Following Taleb’s (2007) terminology, the latter are also referred to as “Black Swans” (see Taleb, 2007).
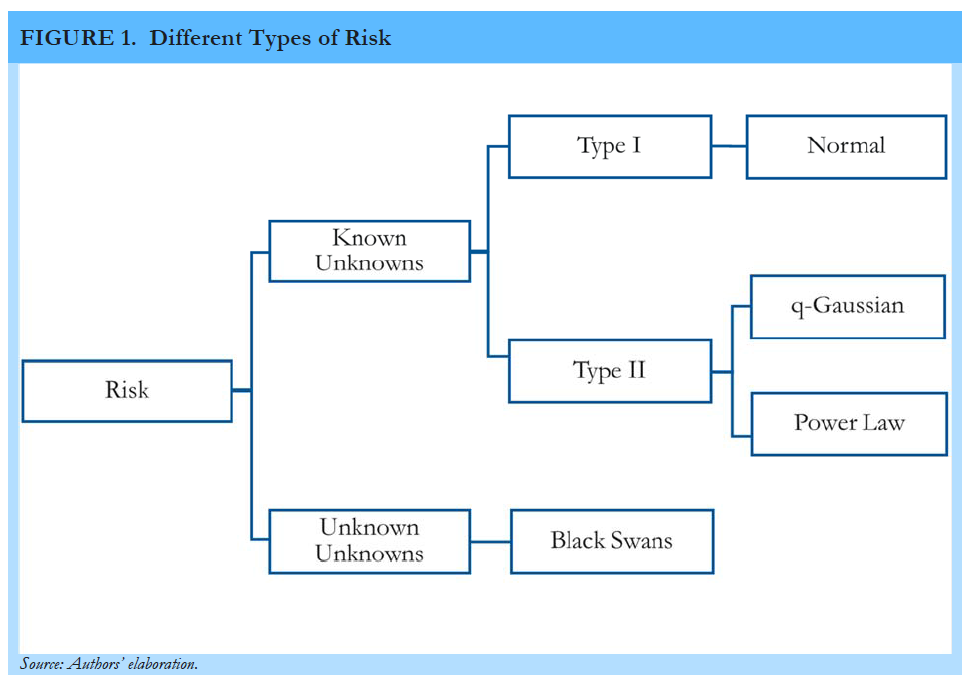
While insurance tends to be among the most efficient tools against risk, an important message of the study is that not all risks are insurable. Specifically, given their unpredictable nature, Black Swans are uninsurable. A good example is 9/11. Nobody could have predicted on 9/10 that 9/11 would happen so an insurance contract against that risk was ex-ante unconceivable. To minimize the impact of such events, emerging markets need to rely on other risk-management tools such as building resilience through better infrastructure, regional trade agreements, and diplomacy. The quick deployment of ex-post aid is another key component in the emerging markets’ arsenal against Black Swans.
Risks with known probability distributions (known unknowns) are typically insurable, depending on their specific characteristics. As noted in Figure 1, the report distinguishes between risks with underlying normal distributions (Type I risks) and risks with distributions that exhibit fat tails (Type II risks). Figure 2, Panel A illustrates the archetypical example of a random variable with a normal distribution, human height. Given its well-defined distribution, finding insurance against a bet on the height of the next individual coming through the door should be cheap since the ex-ante mean will give us quite a good approximation. In other words, the probability of finding an individual several standard deviations above the mean is negligible.
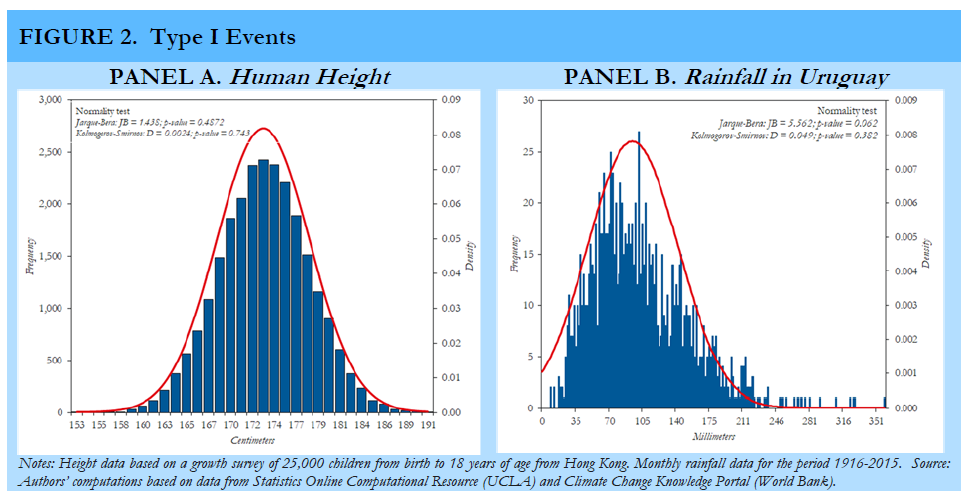
Unfortunately, normal distributions are extremely rare among economically relevant risks. A possible exception, rainfall in Uruguay, is shown in Figure 2, Panel B. Rainfall in Uruguay is critical, among other reasons, because hydroelectrical power plants account for about 60 percent of total energy production. When the country faces a drought, it needs to import more oil to compensate for this shortage. To insure against this risk, the Uruguayan government issued in 2014 a rainfall call option based on a rainfall index as a strike price and barrels of oil as the underlying asset. Type I risks should thus be relatively easy and cheap to hedge using international capital markets.
Most relevant risks for emerging markets are characterized by distributions with fatter tails compared to the normal distribution. These distributions range from q-Gaussians, with similar bell curve shape but fatter tails than those of a normal distribution, to power law type distributions where a large share of the distribution falls under the tails. Risks associated with fat tailed distributions are typically more difficult and expensive to insure.
How expensive or even how much insurance will be available depends on the fatness of the tails. On the one hand, risks associated with changes in international asset prices and commodities tend to follow bell-shaped distributions. Looking at the distribution of the change in oil prices (Figure 3, Panel A), one may think that these changes follow a normal distribution. However, this would be a costly mistake. The key difference between the underlying distribution of oil prices and a normal distribution lies in the fatness of the tails. In fact, assuming a normal distribution, oil traders in 1971 would have believed that an event of the size of the ensuing oil crisis was literally impossible. If those traders had assumed a distribution with fatter tails such as a q-Gaussian, they would have realized that, while rare, such an event was entirely inside the realm of possibility and thus would have tried to protect themselves. Given their relatively thin tails, insurance against shocks to most international traded commodities or assets (see, for example, the distribution of Dow Jones returns in Figure 3, Panel B) should be available and relatively cheap. Although fatter tails increase the risk of extreme events (and hence risk for insurers), the risks are still small enough and can be priced accordingly.
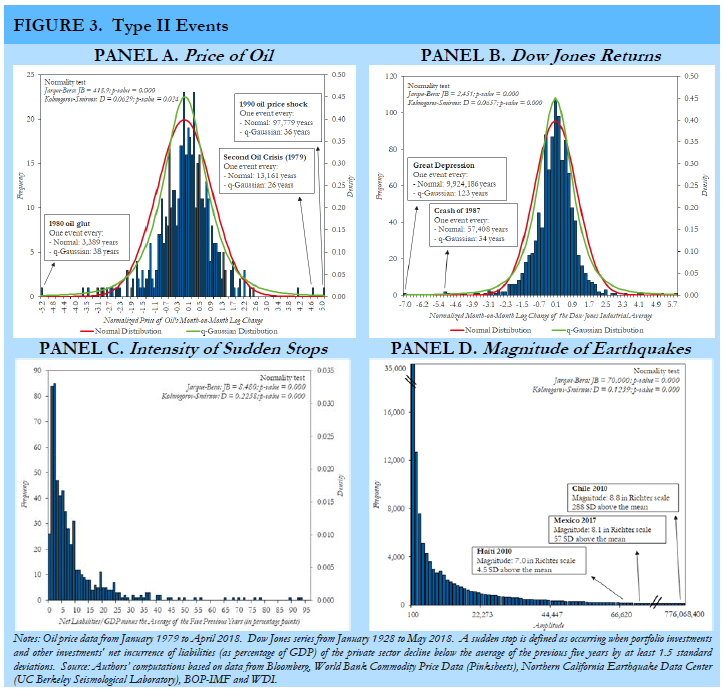
On the other hand, key financial risks affecting emerging markets such as sudden stops of capital inflows (Figure 3, Panel C) or natural disasters such as earthquakes (Figure 3, Panel D) follow distributions, such as the power law, with very fat tails. These fat tails imply that extreme events large enough to change the ex-ante moments of the distribution occur with a non-negligible probability. Insuring against this type of uncertainty becomes much more difficult.
While precautionary savings in the form of international reserves seem to be the only ex-ante solution to the problem of sudden stops (no insurance is available at this date), a quickly evolving insurance technology has started to provide solutions to natural disasters such as earthquakes in the form of catastrophe bonds (cat bonds). Albeit partial at best, cat bonds provide a new form of insurance against these natural phenomena. If the bond is triggered (i.e., if the earthquake occurs), the principal obligation to investors is automatically cancelled and immediately used for relief efforts. One of the most successful and larger examples of a cat bond was recently sponsored by the World Bank and covered the four countries of the Pacific Alliance (Chile, Colombia, Mexico, and Peru). The multi-country structure of the cat bond lowers the cost of insurance as the correlations among events between countries tend to be low.
In sum, insurance should be a key component of the countries’ arsenal to manage their most significant risks. The access and cost of insuring against any specific type of risk will be determined by its underlying stochastic nature. As the tails of the distribution grow fatter, it becomes more difficult and costly to insure and other instruments in the risk management toolbox become more important. While new technology such as multi-country cat bonds has brought partial insurance against fat tail events, we still cannot insure against all risks. This will always be true in the case of Black Swans. Building resilience and improving access to ex-post aid are the only preventive tools available for such unpredictable events.
References
Taleb, N.N. (2007). The Black Swan: The Impact of the Highly Improbable (New York: Random House).
Vegh, C., G. Vuletin, D. Riera-Crichton, J.P. Medina, D.
Friedheim, L. Morano, and L. Venturi (2018). From Known Unknowns to Black Swans: How to Manage Risk in Latin America
and the Caribbean (LAC Semiannual Report, World Bank). https://openknowledge.worldbank.org/handle/10986/30478
This post written by C. Vegh, G. Vuletin, D. Riera-Crichton, J.P. Medina, D. Friedheim, L. Morano, and L. Venturi.
“Black Swans are uninsurable. A good example is 9/11. Nobody could have predicted on 9/10 that 9/11 would happen so an insurance contract against that risk was ex-ante unconceivable.”
Nonsense. The Twin Towers were insured and the claim was in fact paid after 9/11. An attack against the buildings was both foreseeable and foreseen, as the towers had been bombed in 1993 with the intent of bringing them down.
A more compelling example might be PG&E and the Camp Fire. This is a low probability, but extremely high payout event. In some cases, the cost of insurance is so high that the company prefers to internalize the risk, with the understanding that shareholders might be wiped out from a major adverse event.
Steven Kopits I think you’re misunderstanding things. The reference was to 9/11, not the twin towers. The twin towers were part of 9/11, but not all of it. But what the authors are talking about is the difference between “risk” and “uncertainty” (sometimes called “Knightian Uncertainty” after Frank Knight). Risk can be quantified. Risk that follows a normal distribution can be fully described with the first and second moments. Risk for fat-tailed distributions can be quantified, but you need additional moments. Most insurers are concerned with fat-tailed risks, and they are mainly concerned with what happens at the tail of the distribution and not what happens around the mean. But “uncertainty” is different because you cannot empirically quantify the mean or the variance. You can make a wild-assed guess and collect an insurance premium, but that’s not the same thing as a properly quantified insurable risk. It’s just throwing darts and hoping for the best.
The PG&E example is actually an example of fat-tailed event. And if PG&E goes bankrupt and the shareholders are wiped out, all that means is that the shareholders are shielded from the total cost because PG&E is a limited liability corporation. The difference between the total costs and those internalized by the shareholders will spill over as externalized costs; i.e., society ends up paying.
“I think you’re misunderstanding things. The reference was to 9/11, not the twin towers. The twin towers were part of 9/11, but not all of it.”
Even so, 9/11 was far from a black swan. It consisted of a) multiple simultaneous attacks against b) high-profile landmark buildings including c) the World Trade Center carried out d) by means of crashing hijacked airliners into them.
None of these features were unprecedented.
a) AQ had carried out simultaneous attacks before: the 1998 embassy bombings in Nairobi and Dar es Salaam. It had planned others (Bojinka, for example).
b) There had been attacks attempted and completed against high-profile landmark buildings before: the embassies, among others.
c) The WTC had been attacked before, in 1993. It was seen as such a high-risk target that a pre-9/11 report recommended against putting any emergency command centres there.
d) The Bojinka plot in 1995 envisioned the use of hijacked airliners as suicide weapons, including against the CIA building in Langley, VA. (It was also a feature of several 1990s thrillers.)
So the idea that AQ might try to hijack aircraft and crash them into the WTC and other buildings simultaneously was really very far from unprecedented. It was completely in keeping with their history. If you’d been told in 2000 to come up with likely scenarios for AQ’s next major attack, something like 9/11 might well have been the result.
If you’d been told in 2000 to come up with likely scenarios for AQ’s next major attack, something like 9/11 might well have been the result.
But it wasn’t predicted. And if someone had asked you to objectively assign the probability all of those events happening simultaneously, I doubt that anyone could have done so. What was your ex ante probability? Did you warn the appropriate officials years before 9/11? Remember, we’re not talking about whether or not some series of events is imaginable in a movie or novel. I can imagine sharks in the ocean. I can imagine tornadoes pulling cattle up into the funnel. Does that mean I should alert authorities to the probability of Sharknado VII happening for real? Better warn Tara Reid! We’re not just talking about events that we can imagine; we’re talking about whether or not such a series of events can be assigned an ex ante quantifiable probability of happening within a certain period of time. And the authors are not talking about a one-time only single event; they are taking a frequentist approach that defines a probability distribution. You need more than one event to define an empirically based frequentist distribution.
Slugs –
Let me again give you the direct quote from the text:
“Black Swans are uninsurable. A good example is 9/11. Nobody could have predicted on 9/10 that 9/11 would happen so an insurance contract against that risk was ex-ante unconceivable.”
Insurance is ordinarily thought of as against the value of an asset or a revenue stream. You write, “The reference was to 9/11, not the twin towers.” What does that mean? It’s not coherent or comprehensible. You have to insure something. And indeed, the Twin Towers, the principal object of the terrorist act was insured, and insurance against terrorist acts is available on the market. It is not a black swan at all, but rather a class of risk which is routinely covered in the market. As SecondLook notes below, such risks will ordinarily be reinsured, such that the risk to the Twin Towers will be born by thousands of buildings across the globe. There is nothing ‘unisurable’ about it.
There are many risks the probability or magnitude of which are extraordinarily difficult to ascertain, but are insured nevertheless. Prior to the Macondo blowout, what was the risk of a catastrophic runaway well in the Gulf of Mexico? There had really never been one before of that scale, although smaller spills had occurred. What is the risk of a similar event now? It is one in ten years? One in sixty years? One in a thousand years? You really have only a single event, and even we expand the universe to include the North Sea and Brazil, the sample size and duration remains small for events that are presumed to happen in more than decadal time frames. And yet, you can buy insurance if you want it.
I personally do not believe in Black Swans, only the excuses of weak analysts. All risks can be categorized and assigned some probability. The problem is that our time frames remain too short to properly ascertain the probabilities of certain events, to wit, note that the Gulf of Mexico had, I think, three ‘thousand year’ storm events within a decade. Truth is, we don’t know what a ‘thousand year’ event is, because in some cases the data may not go back much before 1980. Nevertheless, insurance is offered and taken, because speculators exist. At some price, you’ll always find a counter-party willing to assume your risk.
Steven Kopits A more compelling example might be PG&E and the Camp Fire.
This actually falls under the actuarial category of “ruin theory.” I’m a big fan of “R” packages. I haven’t used it in a couple years, but there’s a nice package called “actuar” that’s geared towards insurance modeling in “ruin theory.” There’s a good overview of the package in this Journal of Statistical Software paper:
https://www.jstatsoft.org/article/view/v025i07/v25i07.pdf
So, PG&E’s EBT is about $2 bn.
A event like the Camp Fire could cost $50 bn. What time frame probability do you want to assign it? It never happened before. So maybe 50 years, arbitrarily? So that would be an insurance premium of $ 1bn / year, about half of pre-tax profits. Do you think the regulators would let PG&E raise their rates to permit the company to buy such coverage? I doubt it.
To me, that’s a more Black Swan-like, because — to the best of my knowledge — we’ve never had such an event before. So the probabilities and magnitudes are mostly finger to the wind, but certainly not impossible to estimate (and someone actually did that, if you cared to comb through PG&E’s records). But it’s not that which makes it difficult to insure. It’s that the cost of the premium is material to the entire financial structure of the firm. So there’s tendency to self-insure, as did BP in the Gulf.
Steve Kopits These two statements are inconsistent:
To me, that’s a more Black Swan-like
and…
but certainly not impossible to estimate (and someone actually did that,
If something can be assigned an ex ante probability distribution, then it is not a Black Swan event. The probability of the California fires was predictable. We have plenty of historical data on fire frequencies and acres burned. More than enough to describe a probability distribution. If you get the probability distribution right, then you can predict tail probabilities even without any actual history of that tail probability. The whole point of fat-tailed distributions is to look at tail probabilities.
But it’s not that which makes it difficult to insure. It’s that the cost of the premium is material to the entire financial structure of the firm.
I don’t think that’s the point. Whether or not a company buys insurance or chooses to self-insure is just a business decision and isn’t really germane to whether or not an event represents risk (what the authors call “Known Unknowns”) or uncertainty (what the authors call “Unknown Unknowns”). Risk is quantifiable; uncertainty is not. And the authors aren’t terribly interested in “Black Swans” or “Unknown Unknowns”, which is what a lot of the comments are about. The authors are really interested in the difference between what they call Type I and Type II risks. My takeaway from their post is that when it comes to economic phenomena we should pay more attention to fat-tailed probability distributions and less attention to thin-tailed distributions like the normal or t-distribution.
Slugs –
You can give an ex-ante probability distribution to anything. You just don’t know if it’s true. What are the odds of another major oil spill in the Gulf of Mexico in the next twenty years? Who knows? I think it’s low, but so did BP before it blew up the Deepwater Horizon.
As for fire risk, it is not the risk of a California wildfires, which happen every year. It’s the risk that PG&E starts a wildfire which generates losses of more than, say, $10 bn. That’s the risk. And I am guessing that some analyst at PG&E actually ran that number and showed it to management, and the respective manager probably asked, rhetorically, “Do you suppose CPUC would allow that in our rate case? What’s that, a 6-7% increase, maybe a one and a half cents, in rates to customers? Don’t see it. Well, let’s hope we don’t burn anything down.”
I think that’s what happened, at some point in the past.
Steven Kopits You can give an ex-ante probability distribution to anything.
Sure, but it would be stupid and not based on anything meaningful. I can say that the ex ante probability of Sharknado VII happening is 34.68%. It’s a completely made up number based on nothing, but that doesn’t stop me from making that claim. Hopefully it’s just as obvious that what we’re really talking about is whether or not you can objectively appeal to some actual data.
It is a very nice paper, however, in the reinsurance industry it would be filed under normal good practices.
Or a friend of mine like to say: those O and O’s – outliers and outres, the morning cereal in the business.
9/11 was not a black swan event and Taleb himself has said so. Not only had there been the earlier attempt to bomb the Twin Towers, which were insured. Tom Clancy was publicly furious over the insufficient efforts by US officials to prevent 9/11, which he had pointed out the high probability of in his best selling novel, Debt of Honor, which had a fanatical Japanese using a commercial airliner to crash into the US Capitol building during a SOTU speech, killing off most of the top officials of the US government.
Taleb himself also said that the housing crash and Great Recession were merely fat tailed grey swan events that many were forecasting. The one day market crash of over 20% on Oct. 19, 1987, was completely unexpected and a black sawn event, according to him.
Barkley 9/11 was much more than a few plane crashes. Yes, the buildings were insured, but those insurance costs were a miniscule part of the total costs. No one insured the lives of the people who were killed. That’s why the government had to create a Special Master to handle uninsured claims. And if you could predict that A-Q was going to crash into buildings and kill 3,000 people, then you should also have been able to predict that the US would fight a war costing trillions. Indeed, predicting the likely US response would have been far easier than predicting the attacks themselves. 9/11 isn’t just planes crashing; it’s a whole cluster of events. And as I recall Taleb has a lot to say about clusters.
I’m unimpressed with Tom Clancy’s outrage. There’s a difference between imagining a storyline and having actual quantifiable predictions based on data and not Hollywood scripts. As far as I know Clancy never assigned an actual probability that was at all actionable. And he got the details quite wrong. The attackers were Arabs, not Japanese and the US Capitol was not hit and it wasn’t during a SOTU speech.
I think Taleb’s position on the Oct 1987 crash is a little wishy-washy. Here’s what he says on page 272: If you know that the stock market crash can crash, as it did in 1987, then such an event is not a Black Swan. The crash of 1987 is not an outlier if you use a fractal with an exponent of three. If you know that biotech companies can deliver a megablockbuster drug, bigger than all we’ve had so far, then it won’t be a Black Swan, and you will not be surprised, should that drug appear.
Thus Mandelbrot’s fractals allow us to account for a few Black Swans, but not all. I said earlier than some Black Swans arise because we ignore sources of randomness. Others arise when we overestimate the fractal exponent. A gray swan concerns modelable extreme events, a black swan is about unknown unknowns.
Part of the problem is that there are really (at least) two kinds of “unknown unknowns.” One kind is that we simply don’t have enough data to estimate the minimum number of moments around a probability distribution. This is uncertainty. This is the kind of problem you might encounter in nature. The other kind of “unknown unknowns” arises more from game theory than nature. The problem is that you’re not just wrestling with nature, but with human actors that can behave strategically. So even if the government heeded Tom Clancy’s warning and secured airplanes, terrorists would simply react and adjust their tactics. In that world you’re no longer talking about probability distributions, but who can be more imaginative. That’s also a problem with a lot of economics; e.g., the famous Lucas critique. Consumers aren’t just lifeless billiard balls. They react strategically. Taleb’s view on Black Swans is fine if you’re wrestling with nature; but if wrestling with a strategic actor I’d suggest Machiavelli.