Fama (JME, 1984) was published 35 years ago, but the earlier — perhaps the earliest — appearance of the Fama regression is in Tryon (1979). While the puzzle has largely persisted since then, it has seemingly disappeared since the global financial crisis.

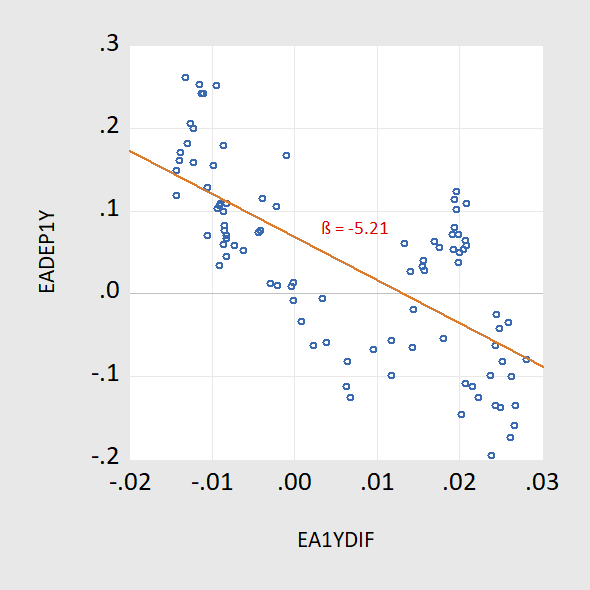
Figure 1: Ex post one year depreciation of euro/dollar up to 2007M08 against one year offshore US-euro interest differential (up to 2006M08). 

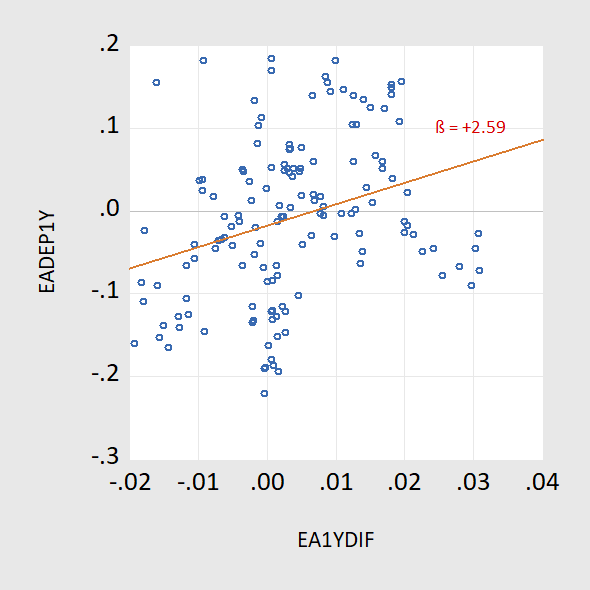
Recall the puzzle: If the joint hypothesis of uncovered interest rate parity (UIP) and rational expectations –- sometimes termed the unbiasedness hypothesis — held, then the slope of the regression lines (in red) would be indistinguishable from unity. In fact, they are significantly different from that value. This pattern of coefficient reversal holds up for other dollar-based exchange rates, as well as for other currency pairs (with a couple exceptions). The fact that the coefficient is positive in the post-global financial crisis period is what we term “the New Fama puzzle”.

Interestingly, after 2006, the relationship flips.

Figure 2: Ex post one year depreciation of eur/dollar up to 2019M06 against one year offshore US-euro area interest differential (up to 2018M06). 

In a revision to NBER working paper just released (No. 24342, posted 12/11), coauthored with Matthieu Bussière (Banque de France), Laurent Ferrara (SKEMA Business School), Jonas Heipertz (Paris School of Economics), we re-examine uncovered interest parity – the proposition that anticipated exchange rate changes should offset interest rate differentials, with data up to mid-2019.

This is one of the most central concepts in international finance. At the same time, empirical validation of this concept has proven elusive. In fact, the failure of the joint hypothesis of uncovered interest rate parity (UIP) and rational expectations – sometimes termed the unbiasedness hypothesis – is one of the most robust empirical regularities in the literature, vigorously examined since Fama’s (1984) finding that interest rate differentials point in the wrong direction for subsequent ex-post changes in exchange rates.

The most commonplace explanations – such as the existence of an exchange risk premium, which drives a wedge between forward rates and expected future spot rates – have some empirical verification, albeit fragile.

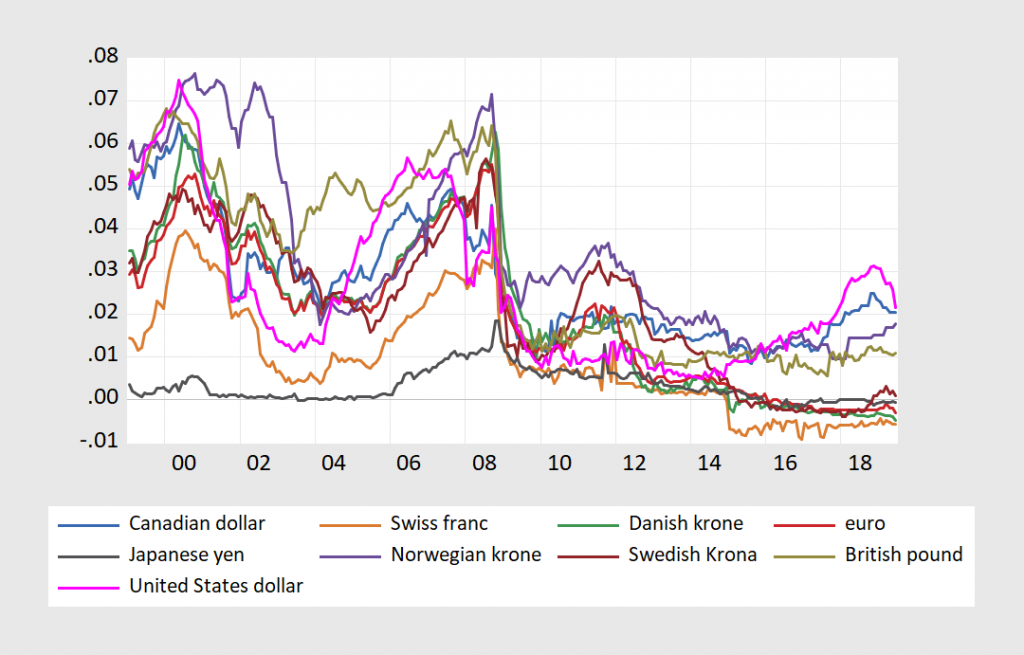
One key development prompts this revisit. First and foremost, the last decade includes a period in which short rates have effectively hit the zero interest rate bound. This point is clearly illustrated in Figure 1 where we plot one-year interest rates for a set of eight selected economies and the US. This development affords us the opportunity to examine whether the Fama puzzle is a general phenomenon or one that is regime-dependent.

Figure 3: One year yields on Eurocurrency deposits.

As shown in Figure 3, more recently — and since the first version of this paper — short rates in the US have risen above the zero lower bound. This allows us to test to the robustness of our findings.

We obtain the following findings. First, Fama’s result is by and large replicated in regressions for the full sample, ranging from 1999 to June 2018 (for exchange rate changes ending in June 2019). However, the results change if the sample is truncated to apply to only the most recent decade, the period for which interest rates are essentially at zero. For that period, interest differentials correctly signal the right direction of subsequent exchange rate changes, but with a magnitude that is altogether not reconcilable with the arbitrage interpretation of UIP. In other words, we obtain positive coefficients at exactly a time of high risk when it would seem less likely that UIP would hold.

The use of survey based expectations — thereby dropping the rational expectations hypothesis — data provides the following insights. First, interest differentials and anticipated exchange rate changes are positively correlated, consistent with the proposition that investors tend to equalize at least partially expected returns expressed in common currency terms (see also Chinn and Frankel (2019) for results 1986-2017).

Second, the switch in the β coefficient at the one year horizon arises because the correlation of expectations errors (defined as expected minus actual) and interest differentials changes substantially between pre- and post-crisis periods. This is important, as can be seen by examining the probability limit of the β’ coefficient in a Fama regression:

s₊₁ – s = α’ + β'(i-i*) + error

so:

plim(β’) = 1 – [A] – [B] – [C]

Where

[A] ≡ cov(covered interest diff.,i-i*)/var(i-i*)
[B] ≡ cov(risk premium, i-i*)/var(i-i*)
[C] ≡ cov(forecast error, i-i*)/var(i-i*)

covered interest differential = – [(f – s) – (i-i*)]
risk premium = f – ε(s₊₁)
forecast error = ε(s₊₁) – s
f is the forward rate for period +1
s is the current spot exchange rate
ε(s₊₁) is subjective market expectations of the future spot exchange rate (proxied using Consensus Forecasts survey data).

The decomposition for the euro/dollar β’ is shown in the Figure 4 below, for the 2003M01-2018M06 period (defined by the survey data). The components are shown as theoretical β’ + [-A] + [-B] + [-C], so as to add up to the estimated β’.

Figure 4: Decomposition of euro/dollar β’. [A] is brown, [B] is blue, [C] is green; black square denotes estimated β’, line at 1 denotes theoretical β’ under unbiasedness hypothesis. Source: BCFH (2019).

Exchange risk comovement with the interest differential does not appear to be the primary reason why the Fama coefficient has been so large in recent years (although the altered behavior of exchange risk does play a role). Rather, how expectations errors comove with the interest differential appears of central importance — that is the [C] component. This correlation changes because in the pre-crisis period, the dollar depreciated more than anticipated, while that is no longer true post-crisis. The size of the swing is partly due to the fact that interest differentials are now less variable (the variance has shrunk).

So far the change has proved durable despite the liftoff of short rates — at least in the US, Canada and UK. Whether this will continue to be the case remains to be seen.

Ungated version of the paper, here.