Steven Kopits opines on statistics:
I don’t like confidence intervals for two reasons:
First, the word ‘confidence’ can be misleading. If the underlying data is bad, if the survey method is weak, if respondents lied, if the sample is not random (but not known to be so), and if the analyst cherry picks data, then the confidence interval can be wildly misleading. If the public reads ‘a 95% confidence interval’, then they think that surely the true mean must be within that interval in all likelihood. But that’s not what the CI means if any of the above mentioned conditions — bad data, bad survey, dishonest statistician — pertains. The only thing is says is that the CI for the calculation for data as it exists and was selected for inclusion yields that particular CI.
The second problem is that a 95% confidence interval is often not actionable. In the example about, the range is from 800 to 8,000. So does one send out the dogs and excavators or not? Can’t tell from the CI. In the real world, CI of this size are all but useless most of the time.
And of course, in a normal distribution, the mean is not only the central value, but also the most likely value.
What’s the alternative to a confidence interval. Maybe a “range”. As I was teaching a review of probability today, I was reminded of this unequivocal statement by Steven Kopits on May 31st, regarding estimates of the Maria death toll in the context of the Harvard study:
Excess deaths in PR through year end, those recorded by the Statistics Office, numbered only 654. Most of these occurred in the last ten days of September and the whole of October. While the power outages there were exacerbated by the state ownership of PR’s utility, a large portion of the excess deaths would likely have occurred regardless, given the terrain and the strength of the hurricane. Thus, perhaps 300-400 of the excess deaths would have occurred regardless of steps anyone could have made to fix the power supply. The remainder can be attributed essentially to the state ownership of the power utility.
I would note that excess deaths fell by half in December. Thus, the data suggests that the hurricane accelerated the deaths of ill and dying people, rather than killing them outright. I would expect the excess deaths at a year horizon (through, say, Oct. 1, 2018) to total perhaps 200-400. Still a notable number, but certainly not 4,600.
See the analysis: https://www.princetonpolicy.com/ppa-blog/2018/5/30/reports-of-death-in-puerto-rico-are-wildly-exaggerated
Notice, this is not a “confidence interval”, it’s just a range, pulled out of the air. I see a lot of this kind of certitude from people who have not learned their statistical theory well. More recently, we have the following results. From Sandberg, et al. (July 2019) in Epidemiology:
Here’s the officially sanctioned (by the Puerto Rico government) report’s estimates (listed as GW displacement in the Table above), as well as my estimates.
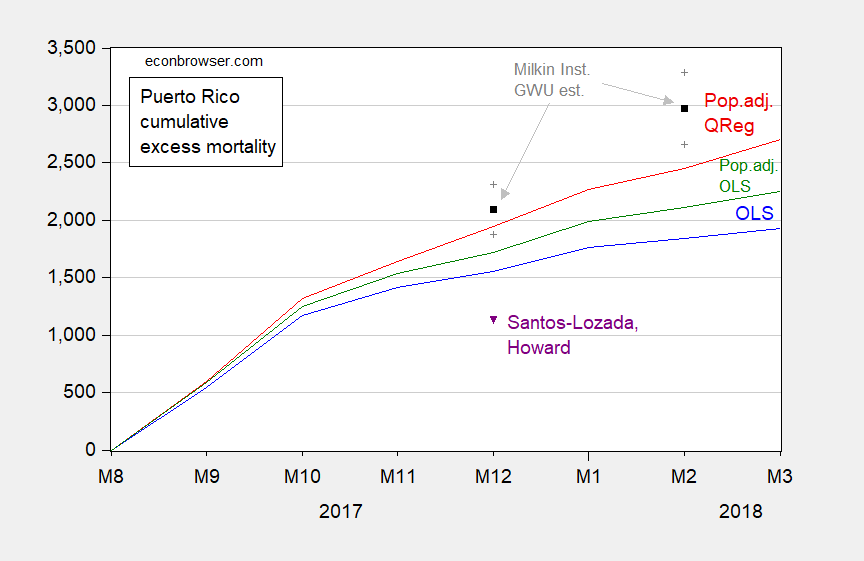
Figure 1: Cumulative excess deaths from September 2017, for simple time dummies OLS model (blue), OLS model adjusting for population (green), and Quantile Regression model adjusting for population (red), Milken Institute point estimate (black) and 95% confidence interval (gray +), Santos-Lozada, Howard letter (purple). Source: author’s calculations in Chinn (2018), Milken Institute (2018), Santos-Lozada and Howard (2018).
Note they are all substantially above Kopits’s range, and even the lower confidence intervals for the Milkin Institute/GWU’s are substantially above the 200-400 range so confidently asserted by Mr. Kopits. On June 3, Mr. Kopits excused his (substantial) miss by asserting that new information had come in:
Of course, this was based on December statistics which were published in the Latino USA article. The May 31 release of deaths revised December up materially, although it did show a decline, as did January. February and March were up. April and May data I think remain too soon to use with confidence. Thus, it would seem that the Oct. 1 number would be higher than expected, but I am unable to make a fixed forecast at this point, as we do not have an unambiguous peak for excess deaths at this point.
But even by May 31, there was widespread knowledge that the count data that Mr. Kopits relied upon was too low, as evidenced by this December 2017 NYT article. That is called “measurement error”. I suppose that we could, like Mr. Kopits, ignore the consequences of such a phenomenon. But I’m pretty sure that’s not the right thing to do, even if it’s classical measurement error (and in this case, I suspect it’s not). [for classical, see this simple exposition]
Bottom line: It’s good to have some statistical theory incorporated into making your estimates and measures of uncertainty.
Additional Kopits comment on confidence intervals:
Were I heading the Harvard study, I would not have used confidence intervals at all. I would have said to my staff:
“So, we’re using an experimental approach that may or may not work. We don’t know if our sample is truly random, and we don’t know if our status as outsiders has affected the frankness of answers given. We think that respondents may have a financial stake in the answers they give. We know that three people in 100 are pretty much nuts, and that we’re trying to find events — deaths — that are comparatively rare, even under the current circumstances. If even 10 people in 4,000 embellished their answers, lied to us because we’re outsiders who came from Harvard and didn’t like us, or believed that they would receive death benefits based on their answers, then we’re going to be way off. So let me help you here. I want this thing caveated to hell and back. This is a good try, an experiment to see if our findings ultimately line up with the recorded mortality data. But remember, our credibility is at risk here. Either people died, or they didn’t. If they did, they are going to show up — every one of them — in the data. If we’re wrong, we’re going to be wrong is a very public way. So, let’s put it out there as a new technique, but let’s not oversell it. Truth is, we don’t know if a survey approach works, and won’t for several months. Let’s put the findings out there, but I don’t want to see anything with the word ‘confidence’ in it.”
By the way, the method used in the Harvard SPH study was not “experimental”, by any means.
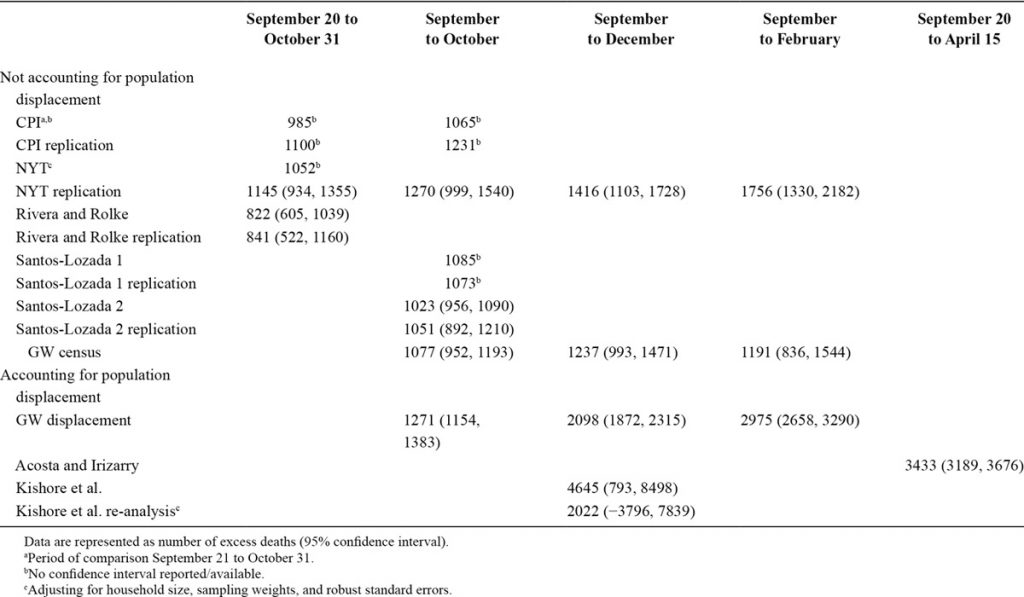
> Note they are all substantially above Kopits’s range,
One might wonder why did he decide to criticize confidence intervals.
surely, if methods with clearly defined assumptions don’t give the results one confidently pulls out of his ass, one would start playing with sophisms to explain why everybody is wrong.
“You are all shit and only I am d’Artagnan” as a common runet meme says.
Gee – Stevie boy picks on “bad” data. Seriously Stevie – there is a plethora of discussions in the statistical literature that addresses what little you have babbled about. Try catching up on your reading. Of course anyone that has “confidence” that Stevie would even understand what this literature has to say is rather foolish.
And while you are at it, remember that Kopits discounts “excess deaths” as simply “premature deaths.” They were old people who going to die anyway. So never mind.
1. Wide confidence intervals are a feature not a bug. They tell you that based on the information provided, no actionable decision can or should be made. A point estimate can be misleading.
2. Intervals account for all the uncertainty that your model includes. To say that they don’t reflect important components of the data generating process is to say that you either couldn’t or didn’t include those things in your modeling. If those external components are important then your intervals and point estimates will be off. But don’t throw up your hands, rather do better modeling.
Ian –
Have you ever actually done a survey? Do you think the Harvard researchers could actually tell if someone was lying to them? Do you think they could really tell if they had a random sample? You’re talking about the difference between ivory tower work where there is nothing at stake and real world situations were huge sums or major executive decisions may be on the table. Not the same thing.
Steven Kopits: I’ve done a survey… reputable political polls are (scientific) surveys. So are (1) the BLS’s CES, (2) CPS, (3) Fed industrial production, (4) Fed capacity utilization. What’s not is Beige Book. I’m pretty sure Ian Fellows knows these things. You should do a google.scholar or SSCI search.
Really? And you came out with a 2x error on the mean at 60 days? You would endorse the study as a good piece of work? That’s the standard you work to?
Steven Kopits: What’s the magnitude of your error on your absolute 200-400 count?
The big problem for our Steven is that on the one hand he accurately warns that having confidence in confidence intervals depends on having believable data and also that it helps to have the underlying distribution be normal. However he then starts positing these arbitrary ranges that both seem to be out of line with the data that comes in later and are also completely disconnected from any apparent underlying distribution.
This sort of resembles his complaint on another thread about EIA oil price forecasts having such wide confidence intervals that they ate “completely uninvestable,” when in fact they may show a reality of data and underlying distributions that suggest that investing in the oil industry is throwing darts at a board, leaving consultants like him having to make up phony levels of “confidence” for the advice he gives to paying clients.
If the best you can do for a client is say that the oil price will be somewhere between $30 – $100, then you are absolutely correct: You don’t have a value proposition and the client is not going to hire you. Nor should they.
I could spend a lot of time on this. Have other fish to fry.
As for the ‘experimental’ data. As I recall, I think it’s in the text of the study, the survey approach was tried in Puerto Rico as a template for estimating mortality in countries were official mortality numbers are not available, eg, Sudan. That’s my recollection.
If the survey was not experimental, and they blew the mean estimate by 2x, the research and report team should be taken out and shot. For a proven methodology to return a value three times the actual over a sixty day period is unforgivable. Well into gross negligence.
So let me say this again: Don’t oversell your findings. Don’t undersell them, either. And that’s not always easy — not even for the pros! Confidence intervals can be appropriate if you feel confident about the quality of the data, the survey methodology, the sampling methodology, and that you otherwise believe you know what you don’t know. If you think, or are unsure, whether you have a GIGO problem, you can qualify work in other ways.
Steven Kopits:Thanks. You are the gift that keeps on giving. I will use your comments (again) in Monday’s class. I will post excerpt of the class notes on Econbrowser. Stay tuned!
By all means.
Here’s the way I would teach it. Almost all consulting contracts have a willful misconduct and gross negligence clause.
Suppose an investor had invested money against Harvard’s numbers. If the actual attributable deaths reached Harvard’s mean, the investor doubles their investment. If if falls to around 1400, they lose their investment. It falls to 1400, and they sue the Harvard team for damages. Were the researchers grossly negligent? And did publishing the confidence interval hurt them or help them in their argumentation? How would the litigant argue the case? The defense?
Steven Kopits: That’s why we distinguish in statistics between statistical metrics and profit metrics. There is a way to apply profit metrics, and this has been done extensively in exchange rate empirics. You should do some research.
I did public offerings.
I’ve had four projects blow up underneath me over the years. Three are in the press. None were our fault.
In one of them involving a Chinese company who made a NASDAQ IPO, our firm could have been destroyed by simply being involved in the litigation — even if we were found blameless. So, yes, that’s the difference with an academic with no skin in the game.