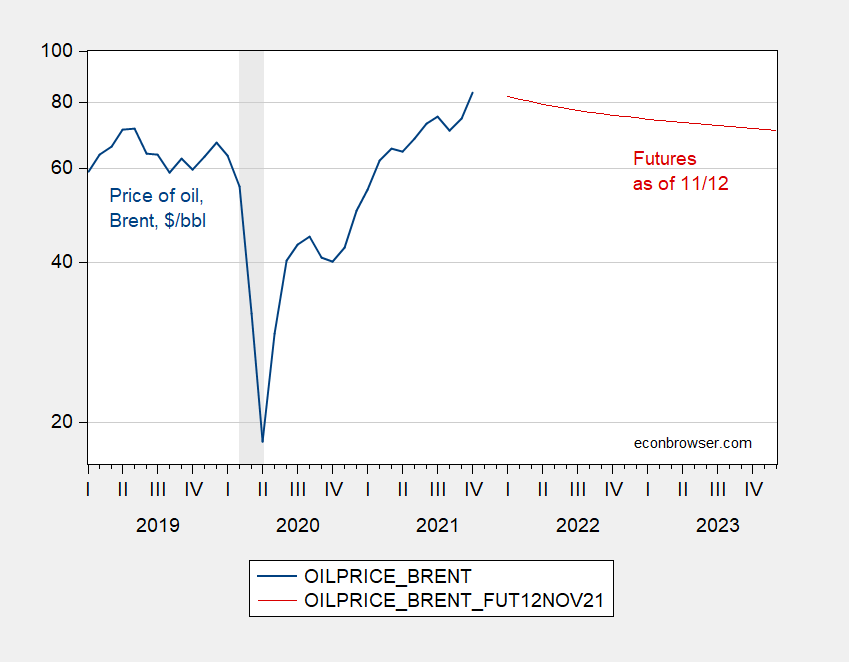
Here’s a picture of Brent (monthly average of daily data) through October, and futures.
Figure 1: Price per barrel of oil (Brent) (blue), and futures contract prices as of 12 November 2021 (red), both $/bbl. NBER recession dates (peak to trough) shaded gray. Source: EIA via FRED, barchart.com, NBER.
Chinn and Coibion (2014) and subsequent analyses find futures do a fairly good job at prediction. Chinn and Coibion examined data up to 2012, for WTI, while Kwas and Rubszek (Forecasting, 2021) examined both WTI and Brent for 2000-March 2021. As noted in this post, futures improve upon a random walk for both RMSFE and direction of change at horizons up to a year.
The DOE’s Energy Information Administration model as reported in the Short Term Energy Outlook reports the following forecast for WTI (as of November 9th):
Source: DOE IEA STEO (November 9, 2021).
So both WTI and Brent are forecasted to decline. How much credence to put in either futures or the STEO forecast (described here)? Miao et al. (Energy Economics, 2017) conducts a horse race of LASSO factor models against various benchmarks, including futures and STEO’s forecasts. Futures and the STEO model do not do altogether badly in terms of the RMSPE’s.

Well, this is consistent with what has happened since just before the end of October, although your figures do not show any actual decline, which has happened over the last three weeks, as I have been repeatedly noting, but the forecast fits with what has happened in those three weeks.
Of course there is some major dealer getting quoted on some sites claiming crude will hit $200 per barrel by end of next year. As our friend who believes that all economists are illogical illiterate innumerate unaccounables would note, standard errors on these forecasts look pretty large.
$200 oil would send the world into recession. It’s not a sustainable number.
What Barkley said: “Of course there is some major dealer getting quoted on some sites claiming crude will hit $200 per barrel by end of next year.”
Only you would take seriously some dude on a weird site.
Check out Kevin Drum’s latest as gold prices went up so you can join the nitwits at the WSJ screaming HYPERINFLATION!
After some notable increases over the last week, gold declined quite a bit today.
@”Princeton”Kopits
We still have roughly 45 days to make your $100 by year’s end prediction. Any updates on your “at least certainly by the year 2080” prediction on the Chinese countryside village proletariat throwing Xi Jinping off the terrace?? Was hoping you might narrow down the time frame slightly.
Steven,
I am not aware that this character is forecasting $200 as a sustainable price, but more like it could get that high. Now is that not more or less the status of your sometimes forecast of maybe $100 by end of this year or perhaps sometime next year, that it will hit that but not stay there? Or are you seriously forecasting a long-lasting $100 or above per barrel price for Brent or WTI? I find that unlikely.
BTW, on today’s Crude Oil Prices site there was a link claiming that both Saudi and Russian figures, including a Deputy Minister of Energy in Russia, are now forecasting crude oil surpluses and falling prices for 2022.
Depends on what happens in the Permian. Within weeks to months of production plateauing in the Permian, oil prices will be back at $100, just as they were before the shale crashed oil prices in 2014. I don’t know when that will be. I presume before 2025.
Who strongly implied that would happen after Memorial Day of this year?? With little argument from his idiot brother-from-another-mother in Virginia?? I’m gonna copy/paste because I know you are the type of slime who takes down posts:
http://www.prienga.com/blog/2021/3/4/towards-100-oil
“This is exactly as we noted in our analysis three weeks ago:
If the trend holds up, the only barrier between us and $100 oil after Memorial Day will be the mood of Vladimir Putin and the goodwill of Saudi Prince Mohammed bin Salman. Both their treasuries are bare. They will be looking to refill the coffers, and not only that, but to buttress their positions against a Biden team less friendly to poisoners and ax murders than the previous administration.”
…….. and continuing farther down:
“At some point, of course, US operators will take the bait. But too late. The Saudi decision to extend the 1 mbpd cut indefinitely can be taken as a declaration of intent — indeed, a thinly veiled declaration of war on the Biden administration — by the Kingdom, and by extension, the rest of the OPEC+ cartel. They are going to keep pushing prices up relentlessly. Pencil in a $10 / barrel rise per month. At that pace, oil prices could reach $100 / barrel during the course of the summer. That’s the message the Saudis and Russians want to send to the Biden administration: ‘Look who has the leverage now.’ ”
“Gasoline prices have already crested $4 / gallon in California and are flirting with $3 / gallon for regular on the East Coast. It will get worse. Possibly much worse.”
“And of course the Fed will have to raise interest rates right into the meat of the stimulus program and a still lingering pandemic.”
“It will get ugly.”
https://www.reuters.com/business/energy/oil-prices-drop-demand-worries-rising-supplies-2021-11-16/ <<——Fascinating
Moses,
At the time I made it clear I viewed Steven’s forecast of the crude price hitting $100 per barrel as not all that likely but not at all impossible. I then also made my point that $40 per barrel was also not out of the question, while not all that likely. You found both of those possibilities as just completely ridiculous, beyond the realm of possibility, despite the history I pointed out of much larger oil price changes happening multiple times in the past in much shorter periods of time.
As it is, we now see Menzie Chinn actually proffering what the apparent 95% confidence intervals were on futures market forecasts in March of this year, about when all this discussion was going on, and they included my outer limit prices, with those intervals certainly taking account of those large and rapid price changes that have happened in the past that I noted. He then noted that as of even now $100 per barrel is within the intervals before the end of the year while the lower one I put out earlier, $40 per barrel, is not any more.
Which brings me to note that in the passage you quoted in your trademark emboldening, always a sign that you think you are scoring some really big gotcha point even when you are not, Steven proved to be right about something, which indeed I have been thinking about in recent months although not said anything about. It is this essentially political matter of both Putin and MBS really not liking Biden, especially compared to their flunky Trump, and so restraining production in order essentially to punish him and hurt him with higher oil prices, which have happened. They do not like him, and since earlier this year prices have moved up quite a bit, if not all the way to $100 per barrel, and I am now suggesting we may have seen the end of that upward movement for awhile. But they did and still are reatrain production in a clearly jointly agreed upon fashion, with this crucial to that price increase that has now put $40 per barrel outside the confidence intervals as at all likely before the end of the year, but still not $100, which I have still allowed as a possibility, even as I note the recent crude oil price declines.
Needless to say, this has made Biden’s call on them and the rest of OPEC beyond KSA to increase production to lower oil prices look kind of pathetic, even weak, given that they, at least Putin and MBS, do not like him, although, heck, I would like to see him tougher on MBS than he has been. He has been reasonably tough on Putin, I think. But indeed, I have noted here already that I had to agree with people that it was rather incoherent of Biden to simultaneously put out this pathetic plea while he was on his way to the Glasgow summit and calling on a lowering of fossil fuel production in the US, including of oil.
So, Moses, this is yet another case of you presenting a bunch of emboldened quotes that simply leave you looking like md needs to send you home from his clearly too successful Error Bar.
Oh, and regarding your bet that you are so proud of, would you really be willing to bet your pension on that crude oil will not exceed $100 by the end of the year? How much would you want to be paid if you did bet your pension and you won your bet? (And, sorry, I am not going in engage in such an exercise as I do not bet on stuff like this as Menzie does not either.) And, of course, this is just hot air as you are not making any such bet that I am aware of for real, no skin in the game for you on all this hot air you are gaseously emitting.
I have to say, I like those quotes.
You should keep in mind that OPEC reads my stuff, too. As do folks on the Hill and at the EIA.
I was too conservative on gasoline prices.
And I believe the Fed will have to choose between inflation and raising interest rates and crashing equity and housing markets. The housing market deflation is already underway in parts of the country. I expect it to become more serious during the course of Q2 — right into the election period.
It will get ugly in all likelihood. I am penciling a loss of 58 seats for the Dems in the House, which would bring them back to the level not seen since 1931. The UK has set the precedent. With the Corbynization of the UK Labour Party, they are now back at their share of seats in the Commons that they held in 1935. I expect something similar here come next November.
Steven Kopits: Aren’t you the same person that asserted no more than 200-400 Maria-related deaths in Puerto Rico?
Just another day in the life of a New Jersey consultant:
https://finance.yahoo.com/news/iea-says-end-oil-price-090000478.html
Now I’m ticked at myself because I paid $2.679 yesterday at the station pump and I could have paid $2.659 today. Uncle Moses screwed up again kids.
“You should keep in mind that OPEC reads my stuff, too. As do folks on the Hill and at the EIA.”
What a self serving arrogant statement! Maybe they do read your worthless blog after all – late in the day when they need comic relief. Just after they read the latest from The Onion!
“Princeton”Kopits says the following: “I am penciling a loss of 58 seats for the Dems in the House” You’ll notice this imbecile who masquerades as an oil consultant is in love with this phrase “pencil in”. Let’s look at another example when Kopits used this same phrase:
“Pencil in a $10 / barrel rise per month. At that pace, oil prices could reach $100 / barrel during the course of the summer.”
Kopits said this on March 4 of this same year. We’ve long since passed by Summer in case Kopits hasn’t noticed. So let’s do some simple math for our village idiot/court jester in New Jersey. The price of Brent at that time (March 4) was $63 (using the lower number that day actually makes Kopits “look better” with this math we are doing). Brent right now, we’ll say it’s $83 even just to make Kopits’ idiocy look as complimentary as we can. that’s a price rise of $20 even, which makes our math quite easy. It’s been slightly over 8 months since his laughable prediction. So get your handy dandy calculator or some scratch paper out and do the math $20 increase divided by 8 months time. That’s a $2.50 increase “per month” when Kopits told us all to “pencil in” $10 increase per month. I guess in an oil consultant’s world that must be like”hitting the nail on the head”. Certainly must get loads of “admiration” from the EIA.
” I am penciling a loss of 58 seats for the Dems in the House,”
a chunk of that is a result of extreme gerrymandering by republican states. this has gotten worse since the voting rights act was gutted. recent republican behavior indicates they no longer embrace the principles of a free democracy.
So, there are different types of forecasts.
There are straight up forecasts: “Front month LLS will reach $97.50 on Feb. 3” That’s an example of a specific, falsifiable number.
There are conditional forecasts of the sort that, say, the CBO might make: “As the law is proposed, the deficit will grow.” Many agencies are saddled with these sorts of constraints, that is, they are given a premise which may not be particularly realistic, and then are forced to make a forecast assuming the particular constraint is true. I would imagine Menzie has had do this sort of thing. We did so for the DOE.
There are projections: “Joe Biden is projected to win Arizona.” This is usually a trend analysis based on historical data. It says, if things go as expected, Biden wins. It does not, however, claim that things will go as expected.
There are scenarios. The EIA usually has three scenarios in its AEO and IEO, with the middle one labeled ‘Reference Scenario”. Usually we treat this as a forecast, but the EIA would claim that it is not.
And then there are all sorts of soft forecasts. I used the phrase ‘pencil in’ to indicate a soft forecast, as when I might say, “Pencil in August 20th for a cookout.” That’s kind of what you are thinking, the the target could still move. The phrase ‘outlook’ has a similar connotation.
And there are even softer forecasts, for example, characterized by phrases like ‘best guess’ or ‘more likely than not’.
So, yes, there are all kinds of different forecasts. ‘Pencil in’ implies a type of soft forecast.
Is that your value-added in this conversation, Menzie?
No worries “Princeton”Kopits, Barkley Junior completely believes you were making a “soft forecast” on $100 oil this year after Memorial Day. Barkley is never happier than when he’s playing Harry Dunne to your Lloyd Christmas.
Moses,
Thanks for confirming with your latest report that retail gasoline prices seem to have dropped in your locale. I am waiting for others here to report to us what is going on with them where they are. And I also thank you for the link to the IEA report that also sees downward pressure on crude prices.
So, it looks that my recent calling out of the likely near term end of rising gasoline prices and a likely lower inflation report next month, still so far unnoticed by most of the media that still today has been ranting about rising gasoline prices, continues to look to be prescient. I remind you and everybody here that I was the first out the door on this, which seems to be getting more and more support.
I have no comment on Steven Kopits’s more recent broader forecasts. His record gets worse as he moves further away from the oil industry, where he is also not always right about things, despite his high level of information on it.
Moses –
Regarding Dem losses: A piece today from the Washington Post..
See the graphs.
https://www.msn.com/en-us/news/politics/democrats-face-a-2022-superstorm/ar-AAQOVnV?ocid=msedgdhp&pc=U531
@ Kopits
I can’t believe I’m even bothering asking you this, but like a fool, I’ll bite. I feel like I’m asking donald trump about nutrition or how to avoid venereal disease. Where/How exactly are you pulling the 58 number from?? I don’t even think you could find someone from the National Review who believes that. Remember, when you say “a loss of” that implies Republicans are taking 58 seats that Democrats currently have. That’s a huge/delusory number.
I think this might give you a better clue what is going on than your WaPo link:
https://projects.fivethirtyeight.com/redistricting-2022-maps/
The forecast is for oil prices to return to pre-pandemic levels. Of course those are some wide confidence intervals so who knows? Oh yea – rsm knows.
Princeton Steve is convinced oil prices will pass $100 some day. Like those authors who in 1999 told us that the DOW would hit 36000 some day.
On the other hand JohnH is 100% certain that the Saudis will keep oil prices down to destroy companies like EOG Resources. Never mind that their stock price is up. What do people investing in the stock market know? After all JohnH thinks he is so much smarter than they are.
So many opinions, so little time!
The usual brain dead response from pgl. No one said that the Saudis would destroy EOG resources. However, a Saudi decision to increase production could sure impact the ROI of frackers and reduce investment. Worse, fracking was never all that profitable to start with, so investors shouldn’t be hard to spook…
“ Normally, a spike in prices induces energy companies to increase production, but not this time. Energy prices fell by as much as 70% early in the pandemic. According to a New York Times report, energy executives are not willing to increase production because they are still experiencing the trauma from the crash, and Wall Street is hesitant to fund exploration because of new pressures to meet climate and ESG (environmental, social, governance) goals.
But the truth is actually less complex: even before the pandemic, shale oil and fracking had not been profitable.”
https://www.barrons.com/articles/why-are-natural-gas-prices-high-because-fracking-isnt-really-profitable-51635439006
Sad it is to have explain basic info to pgl all the time…
“No one said that the Saudis would destroy EOG resources.”
Now you are telling me that EOG Resources had not been making a profit? Damn dude – learn to read a 10-K filing. http://www.sec.gov make this easy.
Yep – JohnH is truly a no one!
‘According to data from Credit Suisse’s HOLT database, North American energy companies had a return on investment below their cost of capital for 21 out of the last 30 years. In other words, 70% of the time, returns were disappointing.’
I know you are research impaired but one can check the financials for EOG on http://www.sec.gov. 30 years ago these companies were not making profits but they have reduced their costs over time and oil prices are a lot higher now than they were in the 1990’s. Your Barrons dude is almost as dumb as you are.
A follow-up on this spin:
“According to data from Credit Suisse’s HOLT database, North American energy companies had a return on investment below their cost of capital for 21 out of the last 30 years. In other words, 70% of the time, returns were disappointing.”
The author failed to tell us what the cost of capital is. I guess he learned finance from Princeton Steve. But since I realize JohnH is too lazy to check the financials for EOG, I did. Over the 2007 to 2021 it made strong profits in all but 3 years: 2015, 2016, and 2020 witnesses losses. So if the Saudis keep the price of oil below $50 a barrel, EOG is going to struggle. Now I ask you – is anyone forecasting such low prices on a persistent basis?
《As our friend who believes that all economists are illogical illiterate innumerate unaccounables would note, standard errors on these forecasts look pretty large.》
Did you forget that all economists are murderers as far as I’m concerned, and I will not rest until the economics profession is dead and buried, like phrenology, or reduced to a joke like Theology?
Are economists so dumb they don’t see backwardation and how you profit by buying futures low and selling them as they rise to spot? Is it possible no economist understands how markets really work, and they spend their time doing the equivalent of arguing about the number of angels that can fit on the head of a pin?
We are murderers? I demand a trial by my peers.
rsm: Without resorting to vitriol, let me say I understand backwardation/contango and why each might occur. I also understand a biased forecast might still be the one with minimum variance. I think most PhD economists who have gone through a Ph.D. level econometrics course would understand this as well.
the vitriol comes from rsm blaming the financial sector for the death of his brother. there is no amount of rational discussion that is going to change his behavior on this blog. he has found his target for blame.
rsm is bringing to remind me of Steve Bannon.
We don’t know the details of what happened to rsm’s brother. Finance guys aren’t exactly known for their great compassion. Or maybe you know something about Boesky and Michael Milken pre- pragmatic image rehabilitation I don’t.
“Did you forget that all economists are murderers as far as I’m concerned,…”
It’s the “as far as I’m concerned” bit that’s funny here. You’re pretty much nobody, making noise in protest of your irrelevance.
rsm,
Ah, as it is, estimates have been made of the probability distribution of futures prices, and Menzie has made reference to this when Moses Herzog challenged me on saying earlier this year that both $40 and $100 per barrel of crude oil were possible by end of this year. Menzie then pointed out that indeed as of earlier this year both of those prices were within the 95% confidence intervals, although by now the lower of those two prices is not anymore. I have pointed out that given that the distribution exhibits kurtosis, those confidence intervals understate the degree of volatility that crude oil prices exhibit.
But then we get that you have sort of gone too far off the deep end to really care about all your arguments regarding “standard errors” except as part of your lunatic murder charge against supposedly illogical illiterate innumerate and unaccountable economists.
rsm,
Oh, I had forgotten that you for some reason blame economists for the death of your brother. Do you want to remind me of your utterlyu crackpot argument for this again?
BTW, I was mocking you when I referred to “standard errors” in connection with futures prices. This is something that is also not a survey, so no standard errors. Now it might be possible to estimate a probability distribution of how accurate past forecasts have been. That would generate a standard error. The problem is that such would understate the degree of volatility of oil prices, which clearly have a lot of kurtosis, aka “fat tails,” so mere variance understates the true degree of non-certainty. But I understand this is beyond you, despite you having a spline in your back and all kinds of rage over your delusion that economists “murdered” your late brother.
BTW, I would be inclined to offer sympathy on the fact of your brother dying, but not if you are going to go around making all kinds of insane accusations of murder. You are making the seriously sick Moses Herzog look like a poster boy for the Wellness Center.
The producers of Me Myself and Irene are looking for a new star to play the lead role. Jim Carey was great in the 2000 movie but I nominated JohnH as he has split personalities down especially when it comes to oil price issues.
When our host plotted real oil prices over time, I simply noted that $3 a gallon is not exactly the highest price we have ever seen. One version of JohnH attacked me for not caring about the average guy as if gasoline prices were way too high.
But then another JohnH decides that since he hates companies like EOG Resources he needs to applaud the Saudis and Russians for keeping oil prices low. Now I simply noted that at $80 a barrel, EOG Resources is doing financially well. So this version of our multiple personality commenter attacks me for being in bed with the shale oil sector.
I would suggest that JohnH makes up his mind whether oil prices are high or low but then I would not want to spoil his chance to get the lead role in this sequel.
Pgl assumes that this all about my preferences. But I am not personally affected that much by energy prices. I probably pay no more than 1.5% of my income on gasoline and heating and cooling my home. So I often just provide information, usually supported by pieces from industry insiders along with a link.
But what was surprising is that a Democratic partisan hack like pgl would be so gleeful that energy prices spiked to $3 a gallon. I mean, when gasoline prices go up, incumbents get blamed, so Biden is in the hot seat. And pgl loves it!!!
The current discontent with rising gas prices should be a lesson to anyone who wants to drive prices up with a carbon tax: the voters will have their revenge. Yet Iran actually did successfully raise gas prices…by offering universal basic income, the equivalent of $16,389.64, well above the standard scheme of $1,000 a month proposed by many basic income advocates. But pgl, our beloved progressive liberal, mocks Iran’s UBI and their virtually unprecedented success in raising gas prices. Iran did what American progressives could only dream of..and pgl mocks them!!!! https://www.weforum.org/agenda/2017/05/iran-introduced-a-basic-income-scheme-and-something-strange-happened/
And then pgl jumps to the defense of frackers, when I noted that energy prices would probably not get much higher (not that I care that much,) because Saudi Arabia and Russia would coordinate with OPEC to increase production, dampen rising prices, discourage new investment in fracking, and lesson the competitive threat of environmentally catastrophic shale. So why is a progressive liberal so intent on defending frackers?
All of which leads to the obvious conclusion that pgl is just masquerading as a progressive liberal, though it’s clear that he’s a centrist (corporate,) Democratic partisan hack.
“Pgl assumes that this all about my preferences.”
This from the liar who attacks others are being uncaring centrists. I never defended frackers and you know that. I do try to report accurate information which I realize you abhor. So continue with your parade of bashing others as you write some of the dumbest things ever.
“So I often just provide information, usually supported by pieces from industry insiders along with a link.”
How did I miss this. Industry insiders? Do you mean people are clueless as Princeton Steve? No you Google for titles you like and never bother checking the credentials of the author. Which is why some of what you link to is written by people almost as dumb as you are.
“Yet Iran actually did successfully raise gas prices…by offering universal basic income, the equivalent of $16,389.64, well above the standard scheme of $1,000 a month proposed by many basic income advocates.”
$16 thousand a month? I do not think so. Other accounts have this at $15 a month. Oh you were doing this in Korean wons. It must be a nice little world when you can just make up claims you do not understand.
I would accuse you of lying again but then stupidity is your excuse for writing such intellectual garbage.
This account puts those rebates at $9.80 per month and not your lie about something over $16 thousand:
https://financialtribune.com/articles/economy-domestic-economy/81477/iran-monthly-cash-subsidies-to-continue
You must have copied and pasted some really bad writing:
“Iran’s nationwide cash-transfer policy emerged out of heavy cuts to gas and bread subsidies made by then-President Mahmoud Ahmadinejad in late 2010. The monthly transfer amounted to 29% of median household income, or about $1.50 extra per head of household, per day. (In the US, that would be an extra $16,389.64, well above the standard scheme of $1,000 a month proposed by many basic income advocates.)”
I know THINKING is beyond your limited abilities but $1.50 a day is $45 a month (a figure Brookings used in a 2011 paper). It is a far cry from $16,389.64 a month. And yet the moron in your fell for this bad writing. By 2018, the figure people used was $9.80 a month. I had earlier said this was $15 a month, which seems to be an overstatement.
Do next time THINK before commenting. Assuming you know how.
Off topic but important. This author argues allowing gangs of racists to own military assault weapons is a very serious threat to our democracy:
https://www.thebulwark.com/prepare-for-the-shock-troops/
wti is sticky at $80, i don’t know why.
a ny grid ‘operator’ did a simulation to prepare for a texas like cold snap this winter in nys.
gas at my pump this am is down .10 off 3.39 recent high.
the “i did this sticker” is visible but the attendants tried to scrape it off……
thank you for the track on brent.
You are saying we have eliminated oil price variability? SERIOUSLY?!
https://fred.stlouisfed.org/series/DCOILWTICO/
WTI reached $80 4 weeks ago. Yep Paddy – you can say this price will be stuck there like forever. Come on dude – stop the trolling.
wti seems pretty stable the past several weeks.
i have no position on future of oil price variabiltiy……
Paddy,
WTI seems to have broken out of that stickiness. Down to $78.60 as of two days after your comment here on this.
Some of the banks are forecasting $100 to $120/bbl oil in 2022. I would require a reasonable forecast of how the pandemic evolves in order to to put any serious weight on these forecasts.
In the meantime, Americans are panicked about high oil prices, again. Excise taxes remain the lowest among the rich OECD club members. There is broad multi-partisan for obesity-sitting-dementia policies.
President Biden, the elected leader of the most culturally superior nation in the world, has adopted tried and true methods from the War on Drugs and the War on Terrorism to combat climate emissions. Dehumanize, demonize, and then interdict supply and distribution. Thou shalt not attempt to use policy to reduce demand or in the case of the War on Terrorism, question kill and take policies.
You would almost think that the Woman of Good is perching on Biden’s shoulder and feeding him instructions on how to make producers in the upstream sector rich.
One thing about Americans is that they understand a good tale about the forces of good versus evil. And are most willing to respond to missives to make upstream and some mid-stream participants very rich.
To be very clear, exceptional American anti-data, anti-science, anti-technocracy preferences are not just a Trump movement phenomena.
With all the stupid ranting going on of late, I guess you did not want to be seen as lagging behind the rest of these insane fools. Geesh!
Sorry, but crying about mythical anti-science or data fantasies when the Democratic party refused the benefits of natural immunity expose the shallowness of your post.
Oil is not heading to 100-120 because of production creep. For oil producing countries 65-75 oil is the sweet spot. 100-120 means losing control to sour crude countries like the US….and yes, Venezuela.
GREGORY BOTT: I don’t recall the Democratic Party as a whole declaring no benefits to acquired immunity from catching Covid-19. I do remember lots of people indicating that (1) vaccination would likely be more effective against catching Covid-19 than relying on natural immunity, and (2) vaccination would obviate the need to “roll the dice” on getting Covid-19 to get immunity from Covid-19.
Betcha if we exposed everybody to smallpox, then the remaining smallpox survivors would have more immunity than those who never got smallpox. However, I suspect that would be small comfort to all the dead people.
“when the Democratic party refused the benefits of natural immunity ”
bot, this is a silly comment. but let me elaborate. it is not that democrats refused the benefits of natural immunity. it is that the republicans refused the cost to acquire that natural immunity. there was a cost to the weeks long hospitalizations. and given a high r value during the depths of the pandemic, there was the cost of excess spread of the virus through the population that inevitably occurred while achieving this natural immunity. none of these costs are incurred by developing immunity through vaccination. what a stoooopid argument you were making bot.
1. Strip was backwardated even at height of summer 2014. CLZ1 was $87, while prompt over $100, in JUL14. When Hamilton made his “hundred dollars to stay” comment. Regardless of the (later shown very poor) prediction, thought it strange that James didn’t discuss the futures market at all. Whether to disagree, say it supported him, or whatever. Strange for a Bayesian. Nate Silver would not have done same. Also, of course, not just the strip, but the CI needs to be considered/discussed. It’s very evident from the EIA funnel graph that oil prices have (and had) significant uncertainty around the mean. Much more than casual discussion of the mean only, implies.
2. The anti-EMH crowd always emphasizes the lack of perfect forecasting, but this ignores the uncertainty…very well shown in the EIA CI “funnel chart” and derived from fixed prices futures. [Many commenters seem ignorant of this market, don’t realize there is more info than just the strip, that you can bet on fixed price futures.] But of course, lack of perfect prediction, doesn’t justify anti EMH. Look at sports betting. There’s significant variability for a single result. But it would be silly to say that the odds are not overall better than the “I’m smarter” crowd.
3. There’s also an issue of Bonferroni fallacy. Look at enough different metrics, enough different time periods. And then say EMH doesn’t work. But a stronger case really is needed, especially given the theoretical reasons (arbitrage) for lsupporting EMH.
Kevin Drum reads the Wall Street Journal so we do not have to! Gold prices rally – HYPERINFLATION! Yes the WSJ freaks out. Of course Kevin puts this daily price increase in historical context:
https://jabberwocking.com/yet-more-inflation-hysteria-from-the-wall-street-journal-today/
4. I like your use of Brent. It’s not as convenient for long time series of course. And also, important to label clearly. Because news stories and casual discussion in the US, assumes WTI. One more nit about “hundred dollars here to stay” was not citing which index. But Brent is the better world price. Especially Atlantic basin. (Can get some spreads with Asia of course, and there is a need for an “east of Suez” index. ) The problem with WTI is that it is inland from the coast. This seems trivial but has been very significant in the past, with pipelines from OK to the GOM as a bottleneck. Also, during the shale revolution and before the export ban was eased, there was an issue of stranded production because of trade restrictions. All that said, it’s not usually that huge a difference. Few bucks. Also can look at WTI-Houston, more recently. Not that well traded, but useful in assessing spread from GOM to OK. One other issue with Brent versus WTI is that the latter remains the more heavily traded index. And Brent has had some issues with physical supply/definition as North Sea declines. All that said, Brent remains a great index/market with heavy trading.
5. One other thing to note is that there is implicit ability to time arbitrage. So, storage cost and time use of money are a rough proxy for how backwarded or contangoed your strip can get. Yes, we did have that crazy blowout where WTI went negative, but it was near a contract closeout. And happened with WTI only, not Brent (where tanker storage is readily communicable with the market, unlike the Cushing tank farm).
“Can get some spreads with Asia of course, and there is a need for an “east of Suez” index.”
It is called Platt Dubai.
Yeah, I know that index. It’s there and you can (and should) look at it. It’s not as good an index as WTI or Brent though in terms of traded volume, delivery liquidity, etc.. Here’s an article from 2014 on some of the historic and current (at 2014) issues: https://www.oxfordenergy.org/publications/oil-markets-in-transition-and-the-dubai-crude-oil-benchmark/
Again, completely agree that it’s the normal “Asian index” (although you get a fair amount of people referring to Brent also, if you talk to Asian purchasers). I wasn’t trying to say there was a lack of any indicators. After all there are a gazillion indices out there. But they are not all great markets.
Thanks for the link to that paper. Will check it out.
https://www.cmegroup.com/markets/energy/crude-oil/dubai-crude-oil-calendar-swap-futures.html#
Make that Dubai Crude Oil (Platts). This link shows their future prices which are also predicting that oil prices will fall.
Well, as Menzie well knows, this Joe Six Pack cannot resist putting up his single useless data point in the gargantuan pool of oil/gasoline price data. I have to type gasoline instead of gas because Barkley Junior thinks people get natural gas at the station pump, so using the term gas throws him into a whirlpool of confusion. I guess this is completely understandable given that so much natural gas leaves Barkley’s mouth. I got my gasoline at the station pump for $2.679 today (Monday morning). Yes, I know my region has lower prices than the national average.
Herzog,
Um, I usually say “gasoline” but sometime slip and just say “gas.” But the question is, which your report on your local gasoline price does not answer, is how does this price you report compare to what it has been recently? We have not been keeping track. I have been pounding away on how crude prices have been decliinng for three weeks and that gasoline prices appear to have stopped rising and may even be declining a bit in some places. I asked people what has been happening to gasoline prices in their locales, and your report does not answer that question, basically useless, as you mostly are. How your price compares to those in other regions is of zero interest, at least in this discussion.
As it is, the media is continuing with its inflation hype, with front page stories in WaPo about how Biden is obviously losing it because he is not “dealing with” or “confronting” supposedly rising gasoline prices, which indeed were the leading driving force of last month’s inflation report. Are you going to join those who say that indeed gasoline prices are still surging and I am just misguided in pointing out that ctude prices have been falling and maybe gasoline prices have stopped rising? Are you so into your siick vendetta that you are going to replicate your infamous denunciation of my for being the first out the door in noting that consumption growth in May, 2020 set an all time record, which Menzie had to correct your incorrect blast as being false?
I most definitely am the first one out the door here on noticing that these supposedly surging gasoline prices appear to have largely stopped doing so, instead choosing to make silly wisecracks about me saying “gas” rather than “gasoline” a couple of times. have you been spending too much time macroduck’s new Error Bar again? I hope he has some stuff for you sufficiently inexpensive to keep your dad happy.
Herzog,
I just checked my entry on a previous thread where I made my inquiry that you have failed to reply to fully about what is going on in various readers’ local gasoline markets. In fact I used the word “gasoline” in that comment, not “gas,” so this really does look like you are seriously out of it with your vendetta again, I think it is time for macroduck to send you home from his wonderful Error Bar.
@ Menzie
Barkley Rosser has informed us earlier in the year that oil prices could be as low as $40 and that it would not be surprising at all if they got over $100 before year-end 2021. I assume you passed this on to all your former students who now trade oil options. It’s hard to get this kind of valuable trading data from just anyone you know.
Moses Herzog: The EIA STEO forecast of March 2021 indicated the 95% confidence intervals for futures encompasses $40. Given the highly price inelastic nature of oil demand, I don’t see why it couldn’t have happened. It wasn’t my baseline, or even in my 60% CI, but for the same reasons, I wouldn’t have ruled out $100 at the time — or for that matter $100 as of the November 9th STEO.
“I wouldn’t have ruled out $100 at the time — or for that matter $100 as of the November 9th STEO.”
Do me a personal favor, as I know you are a great American, and as I treasure your future health, happiness, and well-being: Don’t bet your WRS pension on it.
Moses Herzog: I don’t bet at all. However, as a social scientist, I have to rely on what they data, and statistical analysis, suggest to me to guide me on my forecasts and accompanying confidence intervals.
just looking at the price behavior from the graph above, it is not unreasonable at all to see $20 swings in oil price over a 6 month time period. this has occurred several times since 2016. since we are at $80 today, it is not improbable. not saying it will happen. but as menzie says, just let the data tell you what it can or cannot do.
@ Menzie
I guess if I was as quick-witted as I often fantasize of being (instead of often thinking of these replies 6 hours later) I would have rather stated/asked…… “So your forecasts and confidence intervals agree with me about the price not exceeding $100 before the end of 2021, if only not in ‘absolutist terms’ ??”
So, Moses, since you seem to be imbibing heavily at md’s worthy establishment, and you are insisting that people bet (I join Menzie in not doing so either, especially not for something with such large variance and even fat tails as oil and gasoline prices), what is your current bet?
I have stated it clearly, I believe for months now, that I did not and do not see it hitting $100 or above before the end of 2021. The fact you can’t get even this simple of a statement clear verifies your intelligence level.
I didn’t “insist” Menzie bet. Quite the opposite, I told him not to bet on the price reaching or exceeding $100. Which, again, speaks to your intelligence level. I wasn’t aware English was your 2nd language.
Moses,
Right, You, the guy who just falsely claimed I said “gas” when I said “gasoline” and when asked to report on whether or not gasoline prices are rising or not in your area reported on the current price but not whether that was a change or not. Then you tell Menzie not to get on his pension on the crude price going above $100 and he tells you he does not bet at all (which I say holds for me).
Ah, but you somehow think that all this somehow shows me as somehow “verifying” my intelligence level when I have been the first person around here out the door noting that crude prices have been declining at that maybe gasoline prices have stopped rising, even as all the media is ranting about how rapidly rising gasoline prices are tanking Biden’s and the Dem’s ratings. Yeah, just who has been messing up here, Moses, you or me? Your intelligence level has been “verified” as what by all this?
It appears there’s still some sanity left, in our strange little SJWs and Kookville (and nothing found in-between) nation.
https://www.nytimes.com/2021/11/15/us/politics/alex-jones-sandy-hook.html
Financial damages will be decided next year.
alex jones should rot in hell. americans have given their lives to protect freedom of speech. but they expected that speech to be truthful, not full of lies.
Ms. anonymous wrote: “1. Strip was backwardated even at height of summer 2014. CLZ1 was $87, while prompt over $100, in JUL14. When Hamilton made his “hundred dollars to stay” comment. Regardless of the (later shown very poor) prediction, thought it strange that James didn’t discuss the futures market at all. Whether to disagree, say it supported him, or whatever. Strange for a Bayesian. ”
Was it really “Strange for a Bayesian” with absolutely zero skin in the game aside from idle curiosity? Folks do look at futures and the slope of the curve and they can be important for heavily indebted producers hedging output prices, but are futures a good way of making longer-term general forecasts? Not seeing much evidence to support that implicit claim.
Clearly in Hindsight, Hamilton was wrong but the forecast was understandable in the light of what looked like semi-permanent geopolitical uncertainty in many resource-rich oil producing countries, the high all-in costs of new unconventional petroleum resources as well as higher costs of attaining and keeping the social license/contract to operate. By 2014, there was no doubting the importance of ‘above ground issues’ in this game.
Also in hindsight, Hamilton should have perhaps focused on marginal costs and technological innovation as well as the ability of the US financial street to persuade clients to go all-in on an unconventional resource that relied on a still yet to be proven extraction technology that ultimately destroyed much wealth during the learning-by-doing process.
Were Hamilton and others looking at new 3D seismic techniques? The potential for directional drilling techniques (with and without using hydraulic fracturing) to reduce costs? Were folks focused on declining costs in the bitumen and other heavy oil extraction sectors? Were people looking at how oil producers could cut emissions and reduce unit production costs at the same time? Were improvements in offshore drilling methods taken into account? These are all easy hindsight calls.
One should be careful not to repeat the same forecasting mistakes made by Malthus in the 18th century and the Club of Rome in 1972. Never underestimate the potential for technological innovation.
Ms. anonymous wrote: “1. Strip was backwardated even at height of summer 2014. CLZ1 was $87, while prompt over $100, in JUL14. When Hamilton made his “hundred dollars to stay” comment. Regardless of the (later shown very poor) prediction, thought it strange that James didn’t discuss the futures market at all. Whether to disagree, say it supported him, or whatever. Strange for a Bayesian. ”
Was it really “Strange for a Bayesian” with absolutely zero skin in the game aside from idle curiosity? Folks do look at futures and the slope of the curve and they can be important for heavily indebted producers hedging output prices, but are futures a good way of making longer-term general forecasts? Not seeing much evidence to support that implicit claim.
Clearly in Hindsight, Hamilton was wrong but the forecast was understandable in the light of what looked like semi-permanent geopolitical uncertainty in many resource-rich oil producing countries, the high all-in costs of new unconventional petroleum resources as well as higher costs of attaining and keeping the social license/contract to operate. By 2014, there was no doubting the importance of ‘above ground issues’ in this game.
Also in hindsight, Hamilton should have perhaps focused on marginal costs and technological innovation as well as the ability of the US financial street to persuade clients to go all-in on an unconventional resource that relied on a still yet to be proven extraction technology that ultimately destroyed much wealth during the learning-by-doing process.
Were Hamilton and others looking at new 3D seismic techniques? The potential for directional drilling techniques (with and without using hydraulic fracturing) to reduce costs? Were folks focused on declining costs in the bitumen and other heavy oil extraction sectors? Were people looking at how oil producers could cut emissions and reduce unit production costs at the same time? Were improvements in offshore drilling methods taken into account? These are all easy hindsight calls.
One should be careful not to repeat the same forecasting mistakes made by Malthus in the 18th century and the Club of Rome in 1972. Never underestimate the potential for technological innovation.
https://www.cnbc.com/2021/11/15/burger-king-parent-restaurant-brands-international-buys-firehouse-subs-for-1-billion.html
Burger King merged with Tim Horton’s coffee and then they acquires Popeyes Fried Chicken. Now they own Firehouse subs? Hey – why not monopolize the food industry and jack up prices. WTF is the Justice Department?
I still don’t like paying over $5 for a meal. Especially meals I didn’t make myself (not that am am even an average homecook, but because I can be assured of the “hygienic-ness” of the process. For example I got some Manischewitz saltine (can they be saltines without the salt??) crackers at the grocery store, because even though I kinda guessed they tasted (and they did) like burnt cardboard, I figured since they were made in Israel they were probably cleaner, and I could put good cheese on it to make it taste good. This cr*p of paying $8.50+ for a freaking value meal is for the birds (and I will NOT do it more than once a month, if that) I can still buy pre-shaped Texas hamburger patties 10 of them for $10 and about 6–8 hamburger buns (forgot the number) for under 85cents. I can get a pretty damned good ribeye for around $9 and a chuck eye for lower than $9 (I forgot, maybe $7–$8) What exactly do these oligopolist fast-food outfits think it is about sitting in a drive threw waiting for something a 5 year old can concoct, uuuuuhhh, out of respect to the blog hosts, I’ll say “excites” me??? I can get sunshine at the park, I don’t need to pay $3.50 more for a meal to talk to a down syndrome teenager and some sunshine killing my eyes.
*drive-thru, excuse me