About twenty years ago, while visiting the Research Department of the IMF, Guy Meredith poked his head in my office and wondered aloud whether interest differentials could reliably predict (in the right direction) subsequent exchange rate changes at horizons of three to five years. The resulting paper led in turn to production of this graph:

Figure 1: Panel beta coefficients at different horizons. Notes: up to 12 months, panel estimates for 6 currencies against US$, euro deposit rates, 1980Q1-2000Q4; 3-year results are zero-coupon yields, 1976Q1-1999Q2; 5 and 10 years, constant yields to maturity, 1980Q1-2000Q4 and 1983Q1-2000Q4 (last observation corresponds to exchange rate data). Source: Chinn (2006).
The Fama regression is:
(1) st+k – st = α + β(itk-itk*) + εt+k
Where s is the log exchange rate defined as home currency units per foreign currency unit (e.g., USD per pound for Americans); itk is the interest rate of maturity remaining k, and * denotes foreign (e.g., UK); and ε is an error term.
Properly speaking, β=1 is the joint hypothesis of uncovered interest parity and rational expectations (so that forecasting errors of the exchange rate are true innovations), but “Long Horizon Unbiasedness” wasn’t as catchy a title as “Long Horizon UIP”.
What do the data look like? Here are graphs for UK and euro area (vs. US):
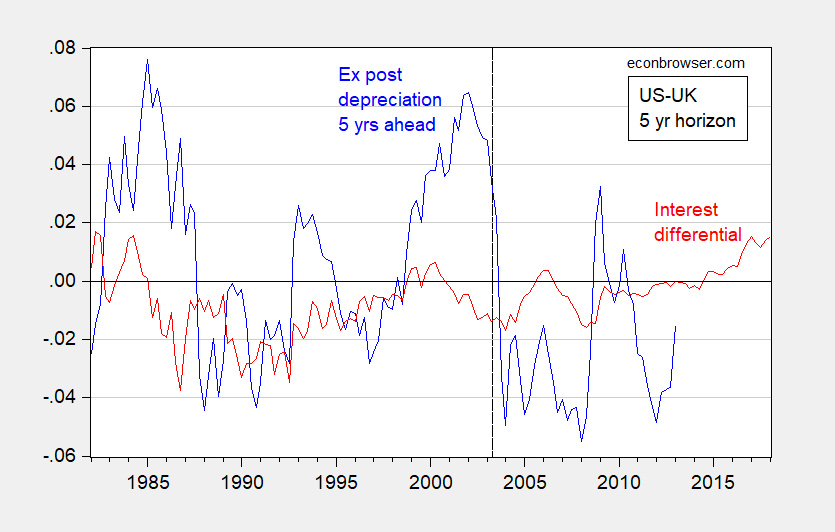
Figure 2: Five year ex post annualized depreciation of dollar/pound exchange rate (higher values denote depreciation of USD) (blue), five year US-UK government bond interest differential (red). The exchange rate depreciation for 2003Q2 pertains the ex post exchange rate change from 2003Q2 to 2008Q2. Dashed line pertains to last exchange rate observation of pre-crisis sample. All data monthly average of daily data for last month of each quarter. Both interest rates constant maturity. Source: Federal Reserve via FRED, Bank of England, and author’s calculations.
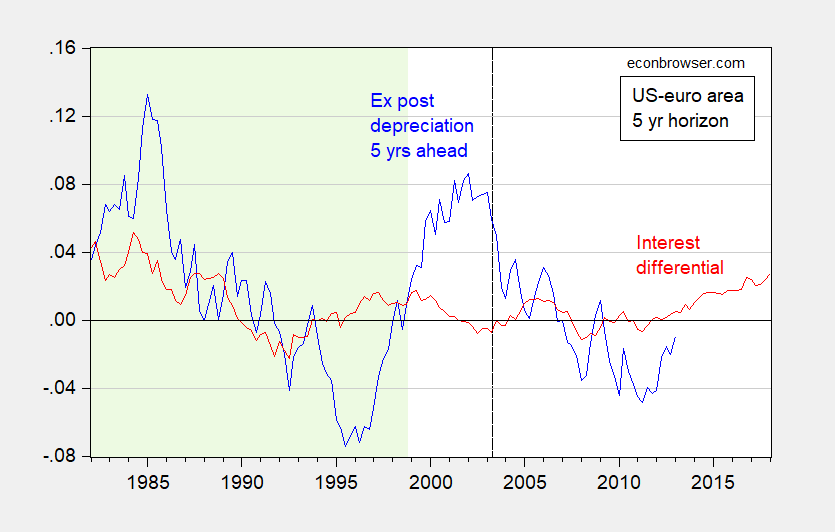
Figure 3: Five year ex post annualized depreciation of dollar/euro exchange rate (higher values denote depreciation of USD) (blue), five year US-Germany government bond interest differential (red). The exchange rate depreciation for 2003Q2 pertains to the ex post exchange rate change from 2003Q2 to 2008Q2. Dashed line pertains to last exchange rate observation of pre-crisis sample. Light green denotes pre-euro area (synthetic euro data used). All data monthly average of daily data for last month of each quarter. Both interest rates constant maturity. Source: Federal Reserve via FRED, ECB, and author’s calculations.
Here are the results I obtained, for the period 1982Q1-2013Q1 (for the interest rates; the exchange rate depreciations are then 1987Q1-2018Q1). I report estimates for β for subsamples before the crisis (1982Q1-2003Q2) and after the crisis (2003Q3-2013Q1). (For an earlier re-assessment, see here; the ending depreciation is 2011Q4, so the last interest rate observation used is 2006Q4).
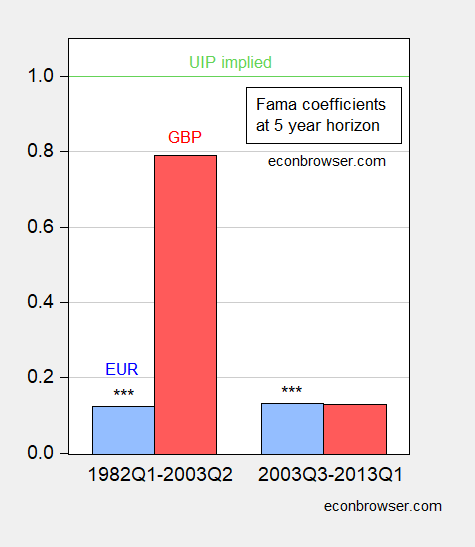
Figure 4: β estimate from equation (1), where t+k is t+20 where frequency is quarterly. Sample period pertains to interest rate data. *** denotes significant difference from unbiasedness value of 1 using HAC robust standard errors. Early euro β estimate incorporates synthetic euro data; late euro β is from a regression including Spain-Germany 10 year spread. Source: author’s calculations.
The euro coefficient in the latter period is negative in the basic specification. UIP relies on default rates that are equal across debt instruments. During the 2010-13 period, sovereign rates for GIIPS countries included some default risk, which would have influenced the exchange rate (recall, we are using German bund yields). Hence, I included the Spanish-German ten year spread to account for this factor, and the reported β estimate reflects this modification.
It would be nice to report that either there were big changes — or no big changes — in long horizon UIP (more correctly long horizon unbiasedness). However, the results are better characterized as ambiguous. For the dollar-pound rate, the point estimate changes substantially; however the degree of imprecision particularly in the latter period means that one can’t reject the null of unity in either case. In addition, one could not reject the null hypothesis the slope coefficient was the same across both periods (although one could reject the null that the constant was the same across both samples). This could merely reflect the low power of the test, when there are relatively few independent observations (recall there are only two completely non-overlapping five year periods in the later subsample, for instance — this is the drawback of using long horizon data).
For the euro, we are hampered by the short sample period (the euro only comes into existence in 1999) and the complications associated with the euro area crisis. I use synthetic euro data to extend the sample, and incorporate the spread variable. A comparison then suggests little change, with the coefficient positive, but significantly different from 1.
In sum, it seems the dollar-pound results are more representative, and indicate continued long horizon UIP. Of course, this is less surprising, in a way, in the latter period given the discussion of the fact that at the short horizon, interest rate point in the right direction for subsequent exchange rate changes, as documented by Bussiere, Chinn, Ferrara and Heipertz (discussed in this post, and this post.)
I ‘m semi-certain that’s the first time I saw the GIIPS acronym used (which is actually semi-amazing as I do read a decent amount of this type literature). I always saw the more derogatory acronym being used. Maybe it shows I was reading way too much of the ZeroHedge blog at that time (I’m thinking 2008–2011 roughly here). Rarely read it anymore. ZH rips off half their sh*t from Bloomberg and the rest is goldbugs and right-wing psychos.
BTW, I found the 2012 Mark and Sul paper (possibly an early “draft”). If anyone is dying to get that (without the paywall), let me know somewhere in this comment thread or the prior post’s comment thread inside of the next 5 days and I will try to have a link up within 48 hours of the request in the same thread.
It never ceases to amaze me the posts that get a big response and the ones that garner less comments. Maybe because it’s midweek people are busy out there. Although there is a heck of a lot to be learned and gleaned here, it seems like you’re implying you took a theoretical bat and only got a single instead of the “home run” you were looking for. But again, even with the theoretical hit only getting you a single, you still learned something in the process.
Your use of German bonds is interesting, because I noticed Jeffrey Gundlach seems to use German bonds a lot as a factor/predictor in what US bonds might do next. Not sure if the choice was for the same reasons–but fascinating to me either way. The safety/security factor makes the USA bonds and German bonds kind of “siblings” in that respect. I think Germans tend to take those things fiercely seriously, for two reasons—just the inherent “stoicism” of the German mindset, and the Pre-World War 2 experiences of Germany. I guess the more pretentious amongst us would call it the “Weimar Republic” years. I just think of it as Pre-WW2 Germany. My Dad was largely German (% of blood) as was his Dad. And my Dad was a Depression baby. I can tell you with all certainty, that if you take someone with a significant % German genes, and then put them through a similar atmosphere as the Depression, it tends to create a certain type of man. And showing softer emotions (at least externally) doesn’t much enter the picture.
Why does UIP hold in the recent period when CIP fails? The failure of CIP is trully remarkable–that used to be the one thing in the textbook that worked!
The GBP does not seem to have such a large cross-currency basis so that may explain it. https://www.bis.org/speeches/sp160608.pdf
Maybe this is why the constant term (whatever that is) is significantly different across periods?
tom: The recent failure of CIP, due in part to newly binding capital requirements, etc., results in fairly small diferentials, relative to the size of forecast errors — at least that is what Bussiere, Chinn, Ferrara and Heipertz (2018) argue.
@ tom
Tom, I really enjoyed the link you put up and it helped me make some connections I wasn’t seeing before. Maybe I can return the favor?? I saw this in the references of Menzie’s paper and thought it might add some insight related to “capital constraints”. Hope it helps.
https://www.newyorkfed.org/medialibrary/media/research/staff_reports/sr393.pdf
Moses,
This is important stuff, but aside from it not being obviously related to the ongoing Trump Show in Washington that always pulls people out to beat up on each other here, this is basically old news, largely a confirmation that out standard models of forex markets do not do very well, although confirming that to the extent they do perform as expected, it is in about the weak way we already knew was the case. So, a worthwhile post, but mostly not really new news.
@ Rosser
I take your point to a degree. But I think things that are “old news” can sometimes be quite educational, and bear being reviewed. Such as the comment I made the other day that Krugman thought DSGE was taking to much prominence over IS-LM and other theoretical tools. Now IS-LM one could argue is “As old as it gets”, but if people get away from it, and stored it in the very bottom of “the tool kit” under other newer tools where it gets lost, some academic may want to reach down under those new tools and show the usefulness of the “old tool”, in which in some ways it becomes “new” in the sense there is still more to be “gleaned” from it that hasn’t been “gleaned” yet.
Rosser, I think you and me probably agree on all this, but I wanted to make that point.
I suspect the main reason this post has less comments (and I am not implicating anyone just because they did not comment this particular time) is that this is a more academically concentrated post, less political, and the usual suspects who belly-ache when Menzie posts something more politically oriented, are the same folks who have absolutely nothing constructive to offer when he posts more “dry” (“dry” to most people’s views not mine) topics on the academic literature.
Barkley Rosser: I would say that the reasons why UIP hold at longer horizons is still up in the air, so that is kinda new news.
I’m still taking “baby-steps” on grasping all of the topic of currencies and exchange rates. But wouldn’t it be self-apparent that if a country (or “economic zone”) stands a significant chance of defaulting, or the currency itself stands chance of losing a large % of its own value, that the rate paid to use that as collateral for a relatively stable US dollar (which is often in higher demand during global crisis) would be much higher than the average market rate??
I’m not trying to be a smart-ass here, I’m asking a sincere/earnest question.
And I know about “carry-trade” but I mean, really?? I don’t think a reasoning person thinks that’s magically going to just suck up all that rate differential.
Still fun and interesting