Today, we are pleased to present a guest contribution by Saiah Lee, Ph.D. candidate in economics at UW Madison.
Central banks make monetary policy decisions based on noisy and incomplete real-time data, and reliance on inaccurate data may yield suboptimal policy decisions. In my new paper, Monetary Policy under Data Uncertainty: Interest-Rate Smoothing from a Cross-Country Perspective, I examine if the persistence in policy interest rates are caused by central banks’ sluggish adjustment in the face of data uncertainty, as conventional belief predicts.
“As a general rule, the Federal Reserve tends to adjust interest rates incrementally, in a series of small or moderate steps in the same direction. … Relatively gradual policy adjustment produces better results in an uncertain economic environment.” – Ben S. Bernanke, May 20, 2004.
This conventional belief can be found in the cross-country estimates of Taylor rules in Figure 1, where the data uncertainty is measured by the standard deviation of differences between real-time data and their revisions after a year. However, this data pattern is not representative of the degree of data uncertainty but rather is an artifact of what we as the econometrician observe from ex-post data.
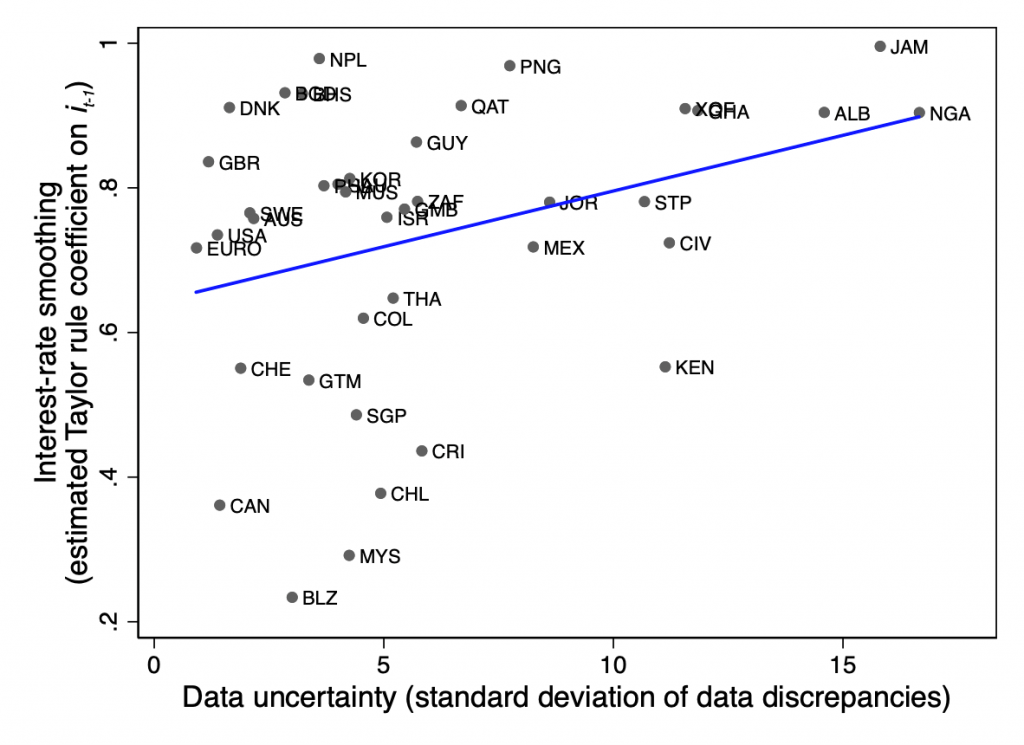
Figure 1: Cross-country estimates of Taylor rules suggest that higher data uncertainty is associated with a more inertial behavior of interest rates. Source: Lee (2018).
The study builds a simplified New Keynesian model and allows central banks to make inferences about the true data from noisy observations using Kalman filter. I find that central banks adjust interest rates less gradually in the face of more data uncertainty, but it creates an illusion of timid and sluggish adjustment of interest rates because central banks’ inference about the true data is not observable to an econometrician in the ex-post data and the central banks’ inferences are highly correlated with lagged interest rates.
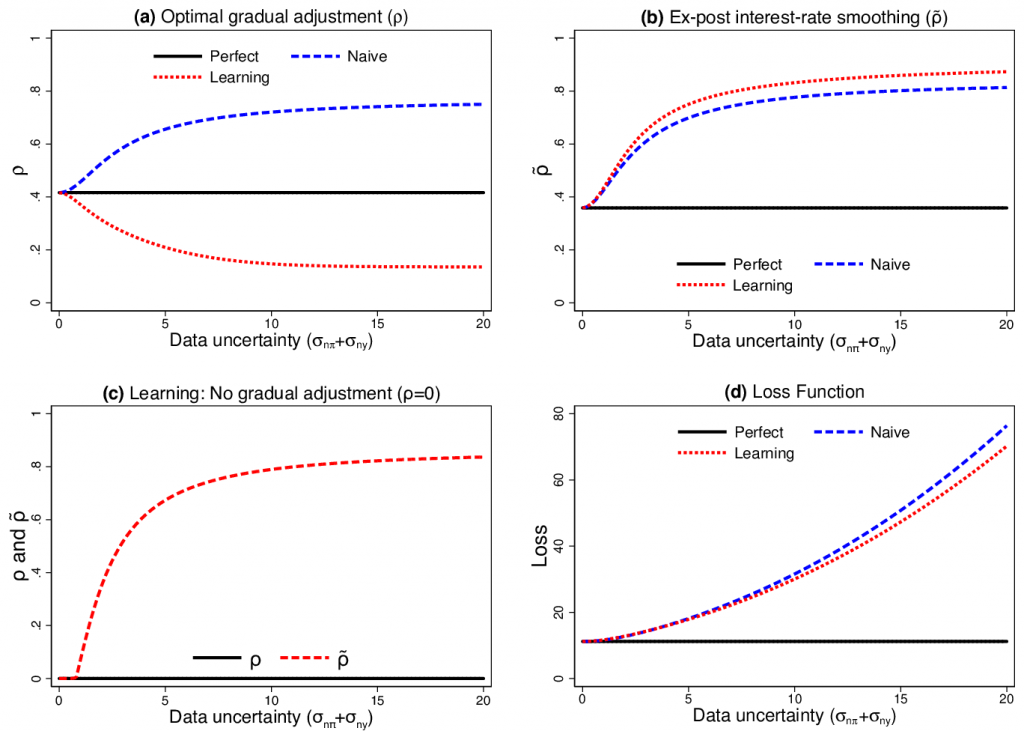
Figure 2: Optimal gradual adjustment versus ex-post estimates of interest-rate smoothing. Source: Lee (2018).
Figure 2 (a) reports the actual central banks’ weight on lagged interest rates, and Figure 2 (b) reports the reduced form estimate of the coefficient on lagged interest rates based on ex-post data. Even if we force the central banks not to place any weight on the lagged interest rates, we have the illusion of timid and sluggish adjustment of interest rates in the face of more data uncertainty, as reported in Figure 2 (c). Central banks’ beliefs about the true data are highly correlated with the lagged interest rates, and they are not observable in the ex-post data.
There are two reasons why central banks adjust interest rates less gradually in the face of more data uncertainty. First, central banks’ learning process effectively, but not completely, filters out data noise. Second, central banks’ learning process helps to tease out additional information about the true data from the persistence of the noise.
The paper is available here.
This post written by Saiah Lee.
Whuuuuuuht??? Phd candidate???? Show off!!!! Damned punk kids. Millennials Shlennials!!!!
OK, what are the odds I can say something intelligent or make “constructive criticism” on a 32 page paper written by a punk kid who is less than half my age and already smarter than I am right now?? Place your wagers kids. I have 5 cans of Mango flavored “bang” drink and 3 cans of back-up cashews. This punk Mr. Lee doesn’t stand a chance!!! I’m braced for it!!!
https://www.youtube.com/watch?v=Zo10xdN2Rds
Is William C. Brainard any relation to Lael Brainard?? Like an uncle or something?? Seems like too much of a coincidence. The name is not that common, yeah??
I met Bill Brainard when I had the honor of spending a year at Yale University’s economic program back in 1980. Bill was one of the few who could challenge the great James Tobin. So some respect:
https://economics.yale.edu/people/william-brainard
I have no clue if he has any relation to Lael Brainard. William Brainard’s paper, “Uncertainty and the Effectiveness of Policy” (1967), opened this literature by providing the classic analysis of multiplicative uncertainty. He shows that when policymakers are unsure of the impact that a policy instrument has on the economy, it may be appropriate for them to adjust policy more cautiously and in smaller steps than would be the case in the absence of uncertainty. (This holds when the policy multiplier and the additive disturbance are independently distributed, but it does not necessarily hold when the covariance between these variables is sufficiently negative.) My paper is more focused on the effect of data uncertainty on central banks’ monetary policy decisions.
I’m still “digesting” the harder parts of the paper and obviously don’t get all the math. It seems the paper is quite well done and what I am not understanding is due to my own weakness in base knowledge level, rather than the paper itself, which seems to be very well done as far as I can decipher.
One question, if anyone cares to enlighten me: The Kalman filter—that is supposed to replicate the “noise” of the economic indicators the Fed is looking at?? I mean here I am assuming “noise” as being a “false indicator” or at minimum a “misleading indicator” that might mislead the Fed to enacting a wrong policy move–and the Kalman indicator created the “speed bumps” in the hypothetical data variation policymakers would be experiencing in real life circumstances?? Am I comprehending that anywhere near to correctly??
PLease be blunt in fact but kind in response as alcohol has killed much of my brain cells over the years.
https://youtu.be/PPKdHP8zWuo?t=52
Don’t everybody answer at once. It’s a cold world out there kids. Learn it early.
Dear Moses Herzog,
Thank you for your interest in my research. The central bank uses the Kalman filter to learn about the true data based on noisy observations. Here is a more detailed explanation:
Referring to equation (28) in my paper, the noisy indicators (Zt) are expressed as the sum of the true indicators (Xt) and noises (wt), where the noises follow MA(1) process. Observing only the noisy indicators (Zt), the central bank makes inferences (X_t|t) about the true indicators (Xt) using Kalman filter before making monetary policy decisions. Referring to equation (30), the central bank observes new noisy indicators (Zt) each period and decides how much weight should be placed on the new noisy indicator (Zt) versus its past belief and information (X_t-1|t-1 and i_t-1). The optimal weight on the new noisy indicator is called “Kalman gain (K),” and it increases as the data get noisier. The central bank’s beliefs are updated every period as new observations come in.
Wikipedia has an excellent explanation about Kalman filter. (https://en.wikipedia.org/wiki/Kalman_filter)
Please let me know if you have any further question. Thank you!
Saiah
@ Saiah Lee
Thanks for not taking offense at my light-hearted teasing, it was meant to bring you smile or maybe even a half-chuckle believe it or not. Menzie is tolerant of my BS I do that mostly humors myself and rarely anyone else.
Believe it or not I had just seen your reply this Friday evening, and it had not updated at the time I made my last comment (no one’s fault, Menzie has a full life and can’t be expected to update the site every 10 minutes). I appreciate the reply. It’s a solid paper. This is a question that has always pesteringly (is that a real word??) been in my head since at least the early ’90s. How the Fed can raise rates to slow down the economy, but it also can be seen as “positive” as market players (those “in the trenches”) think that if the Fed is willing to raise rates that “the economy must be resilient enough fundamentally” to handle the raising of the rates or, “the economy must be resilient enough to withstand the tapping of the brakes”. So it’s a strange but persistent contradiction. Your paper has taken a good segment (though maybe not all, a Herculean task) of the mystery out of that persistent question. I could only dream to have your brains at your youthful age, much less now.
Thank you for sharing with the blog, it was actually a joy (while “all jacked up on ‘bang’ drink” to read your well thought out paper. Saiah, did you know “bang” drink will get you “all jacked up” even more than Mountain Dew?? (mild vulgarity follows)
https://www.youtube.com/watch?v=RLe09qoyPP8
Warm regards, Uncle Moses.
Dear Uncle Moses,
Your humor gave me a big smile on my face during this job market season. I always admire those who have a good sense of humor like you. Thank you for your kind and encouraging words, and please cross your fingers for me. Thanks!
Saiah
Well, Uncle Moses is a tinge sad no one wants to answer his question on The Kalman filter. So Uncle Moses is going to take his homemade Maxwell coffee, grab a semi-large bar of Reese’s peanut butter chocolate and quietly pout there is no Bourbon or liquor in the house, and quietly pout no one wants to answer Uncle Moses’ Kalman filter question and do about a 4 hour “Home Alone” marathon (only 1 and 2 kids, don’t watch “3”). So keep the change, yeh filthy animals……
https://www.youtube.com/watch?v=tpfOhYRYv80